Рассуждения, использующие семантические сети.

Одна из ключевых проблем организации памяти – эффективное управление данными и запросами. При иерархической организации индивидуальные свойства связаны с именами индивидов. Например, индивидуальные свойства Жака (возраст, адрес, семейное положение и т.д.) связаны с именем Жак_2. Кроме того, наследственное свойство связывает Жака с (абстрактным) концептом профессора университета. Выходящие из узла Жак_2 стрелки представимы набором (конъюнкцией) бинарных предикатов:

Возр(Жак_2, 45_лет)Адрес(Жак_2, ул_буля_7) ^

Сем_пол(Жак_2, холст) ^ Конкр(Жак_2, проф_унив).

Эти предикаты указывают, что Жаку 45 лет, он проживает на улице Буля дом 7, холост и принадлежит типу профессоров университета.

Различные имена предикатов, связанные с узлами-индивидами образуют первое множество гипотез (некой теоремы). Например, вопрос об адресе Жака выражается предикатом Адрес(Жак_2, х). Этот предикат составит цель (заключение) теоремы, достоверные гипотезы которой – названные выше свойства Жака. Доказательство сводится к поиску конкретизации для х, позволяющей вывести заключение из гипотез. Проверка показывает, что такой является ул_буля_7.

Иначе обстоит дело с вопросом: «Какой диплом у Жака?», ибо мы не находим гипотезы вида Диплом(Жак_2, …)

Но если воспользоваться связью Конкр, можно получить подходящую гипотезу. Связанная с узлом проф_унив часть графа представима логической формулой:

Конкр(х, проф_унив) 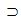(Диплом(х, доктор) ^ Место(х, унив) ^Это(х, проф) ^Это(х, сотр_унив)).

Если добавить эту логическую формулу к множеству (индивидуальных) гипотез, то можно, используя обычную технику доказательства теорем вывести, что Жак имеет докторскую степень. Таким образом, новое множество гипотез и поставленный вопрос составляют формулировку логической теоремы. Исходя из этой формулировки и применяя обычный механизм доказательства, получаем ответ на вопрос.

Механизм доказательства теорем в иерархической среде можно смоделировать следующим образом. Вопрос (составляющий заключение или цель доказываемой теоремы) имеет следующую общую форму.

По-русски: Каково значение некоего индивида по отношению к некоторому свойству?

Логически: Свойство_i(индивид_j, x)

Ожидаемый ответ – конкретизация, представляющая некоторое значение для х. Сначала попытаемся доказать эту теорему, пользуясь лишь гипотезами, прямо связанными с узлом индивид_j в соответствующей графе. Эти гипотезы имеют следующую форму.

По-русски: Значение некоторого индивида по отношению к некоторому свойству есть …

Логически: Свойство(индивид_j, значение_i).

Если так доказать не удается, используем связь Конкр, исходящую из узла, представляющего индивида и указывающего на новое множество гипотез, которое имеет следующий вид.

По-русски: Если индивид принадлежит типу t, то он имеет дополнительное множество значений по отношению к дополнительному множеству свойств.

Логически: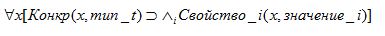

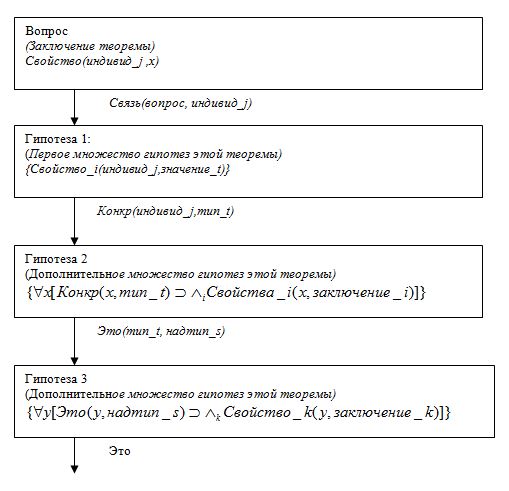
Из этой логической формулы и предиката Конкр(индивид_j, тип_t) выводим новое множество свойств относительно данного индивида. Если эти новые гипотезы позволяют доказать нашу теорему, то доказательство закончено. Если же нет, то связь Это укажет на тип повыше, который в свою очередь даст новое множество гипотез. Эта процедура с последовательными множествами гипотез заведомо эффективнее общего метода доказательства теорем, не использующего иерархической структуры данных. Процедура вывода схематически изображена на следующем рисунке.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.