Представления контекста. Пример введения кванторов.

Представление контекста

Сам по себе концептуальный граф несет немного информации, тогда как включение в семантическую сеть позволяет связать его концепты и функциональные связи с областью рассуждений (экспертизы). Например, Книга_22 – конкретизация слова книга, которое представляет абстрактное понятие (или, иначе, тип). Отношение принадлежности типу представлено связывающим узлом (именем предиката) Конкр (от слова конкретизация). Кроме факта, что Книга_22 относится к типу книга, мы хотим показать, что она принадлежит некоторому множеству книг (например, из библиотеки некоторого университета). Отношение принадлежности множеству представлено связывающим узлом (именем предиката) Элем (от слова элемент). На рисунке конкретизации Жак_2, Кни га_22 и Мари_4

связаны с различными типами и множествами, которым они принадлежат. Отметим, что тип употребляется в абстрактном смысле (абстрактный тип). Утверждения о типах аналитические, например: средний возраст студентов университета двадцать лет.

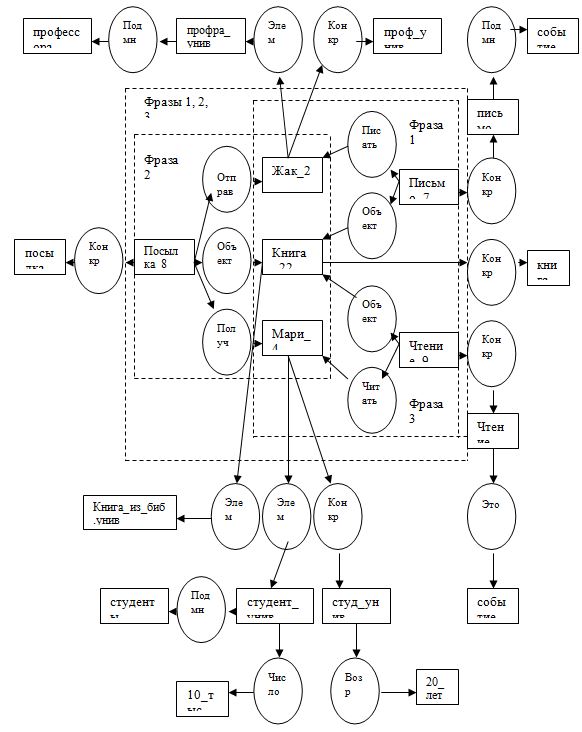
 Наоборот, свойства множеств - синтетические: число студентов университета равно десяти тысячам.

Используем связывающий узел, представляющий имя предиката Подмн для представления отношения между двумя множествами, из которых первое – подмножество второго. Как Элем объявляет о принадлежности элемента множеству, Подмн означает включение одного множества в другое. Элем и Подмн отражают принадлежность множеству.

Связывающий узел Это используется для представления отношения между первым типом и более общим вторым. Напомним, что предикат Конкр когда-то использовался нами для представления принадлежности индивида типу. Это и Конкр отражают принадлежность типу.

Концепты в семантических сетях обладают различными свойствами, делящимися на аналитические (свойства типа) и синтетические (свойства множества). Важно учитывать это различие при построении сетей, чтобы избежать некорректных выводов.

Представление «совокупность – ссылка»

Существует графическое представление (эквивалентное рассмотренным ранее) с узлами, представляющими типы и называемыми «узлами-совокупностями» или «родовыми узлами», представляющими конкретизации типов и называемыми «узлами-индивидами» или «узлами-ссылками»

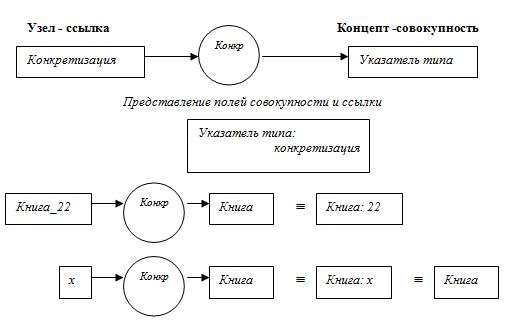
Семантическая сеть образуется последовательностями из трёх узлов, соединённых так: за узлом –ссылкой (например, представляющей конкретизацию Книга_22) следует связывающий узел Конкр, сопровождаемый узлом совокупностью (например, представляющим тип «книга»).

Используя метод Совы, эти три узла можно сгруппировать и представить одним «узлом-прямоугольником», состоящим из двух полей: из «поля-совокупности», содержащего некоторый тип, и следующего за этим полем «поля ссылки», например с конкретизацией типа из первого поля (следующий рисунок). Здесь поле ссылки (справа от двоеточия) представляет тип. Представление [книга: Книга_22] (или короче, [книга:22]) означает вполне определённый объект типа «книга». Представление [книга: х] означает просто какой-то объект типа «книга». Отметим, что наличие переменной в правом поле необязательно. Например, можно заменить представление [книга: х] эквивалентным ему представлением [книга] (рисунок).

Пример

Фразы

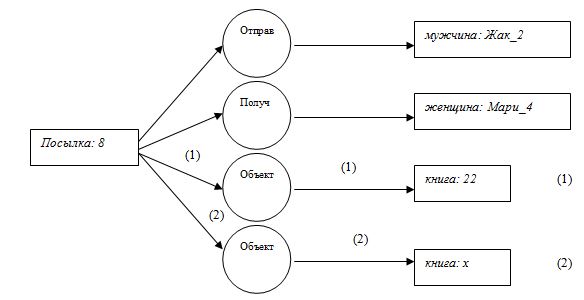
·                         Жак посылает (вполне определённую) книгу Мари,

·                         Жак посылает (какую-то) книгу Мари

представляются двумя графами, которые можно выделить на следующем рисунке: первая фраза – графом без элементов с (2), вторая фраза – графом без элементов с (1).

Пример введения кванторов

Введем графическое обозначение кванторов на примере трех фраз:

·                         (1): Жак посылает (какую-то) книгу каждой женщине,

·                         (2) :Жак посылает всякую книгу каждой женщине,

·                         (3): Жак посылает (одну и ту же) книгу каждой женщине.

Запишем эти фразы в логике предикатов

·                    (1):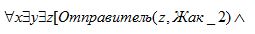

Получатель (z,x)Объект(z,y)

Конкр(z, посылка)Конкр(y, книга)

Конкр( х, женщина)],

·                    (2):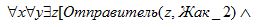

Получатель (z,x)Объект(z,y)

Конкр(z, посылка)Конкр(y, книга)

Конкр( х, женщина)],

·                    (3):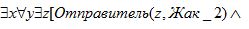

Получатель (z,x)^Объект(z,y)

Конкр(z, посылка)^Конкр(y, книга)

Конкр( х, женщина)],

Перевод с логического языка на графический осуществляется по следующим правилам.

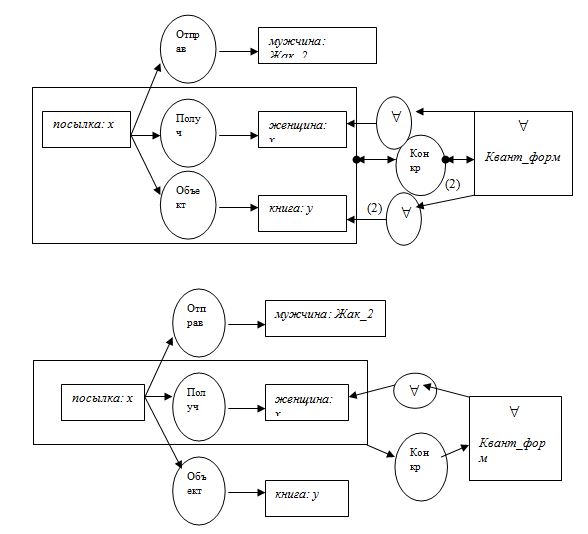
Прежде всего концептуальный граф делят на иерархическое множество зон, каждая из которых соответствует области одного или нескольких кванторов. Например, рассмотрим логическую форму фразы (1). Соответствующий граф изображён на следующем рисунке (элементы с (2) удалить). Для графического изображения нужно ввести обозначение области действия кванторов общности по переменной х. С этой целью установим иерархию прямоугольников концептуального графа. На этом и следующем за ним рисунках жирно выделены прямоугольники наивысшего порядка. Они содержат конкретизацию (Конкр) концепта совокупности «формула под квантором общности» (на последних рисунках, о которых идёт речь, этот концепт обозначен  Квант-форм). Каждая переменная под квантором общности в этих формулах представлена связывающим узлом под знаком .

Читатель может проверить, что с учётом этих соглашений относительно записи предпоследний рисунок, о котором идёт речь, без элементов (2), изображает формулу (1), что он же, но вместе с элементами, помеченными знаком (2), изображает формулу (2) и что последний рисунок, о котором идёт речь, представляет формулу (3).

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.