Главная » Информационные системы » Представление знаний в ИС » Решетки типов, иерархия типов. Определение типа посредством рода и различия.

Решетки типов, иерархия типов. Определение типа посредством рода и различия.

Пусть t1 и t2 – метки типов, если t1  t2, то t1 – подтип типа t2, а t2 – надтип типа t1. Типы «профессор» и «студент» имеют много общих надтипов: «работник умственного труда», «человек», «высшее млекопитающее». В графе «работник умственного труда» - наименьший общий надтип для «профессора» и «студента». Типы « профессор» и «сотрудник университета» имеют общий подтип «профессор университета». В графе «профессор» и «студент» не имеют общего подтипа.

Для преобразования иерархической формы в решётку надо ввести две особые метки соответственно в высшей и низшей точках иерархии – универсальный тип U (надтип всех типов) и абсурдный тип А (подтип всех типов). Иерархия типов даст решётку типов со всеми свойствами решётки:

·                   любая пара меток t1 и t2 имеет наименьший общий надтип,

·                   любая пара меток t1 и t2 имеет наибольший общий подтип,

·                   для любого типа t выполняется соотношение А t  U.

Данное отношение порядка представляется функциональным отношением Это. Конкр означает принадлежность индивида типу.

Решётки множеств и решётки типов

Можно также ввести отношение порядка для множеств (подмножество множества) с помощью предиката Подмн или связывающего узла с тем же именем. При одноэлементном подмножестве Подмн заменяется на Элем. Иерархия типов позволила упорядоченно классифицировать свойства типов, а иерархия множеств – свойства множеств. Следующий рисунок иллюстрирует различие составных частей двух иерархий. Введём на концептуальных графах (в духе классики) несколько функций и операторов, действующих над множеством типов. Прежде всего – функция тип. Она отображает множество концептов на множество Т, элементы которого называются метками (ярлыками) типа. Концепты с1 и с2 имеют один общий тип, если тип(с1) = тип(с2). Денотатом типа t называется множество всех тех сущностей, которые являются конкретизациями некоторого концепта типа t. Оператор, сопоставляющий типу t его денотат, обозначается через Денот. Тип профессор_университета есть подтип типа профессор. Следовательно, денотат Денот(профессор_университета) является подмножеством Денот(профессор).

 

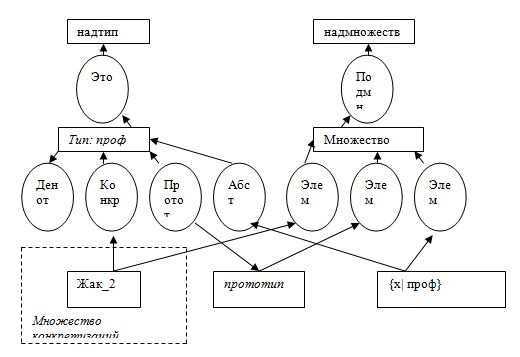
Каждой конкретизации (например, Жак_2) сопоставимо два вида узлов: узел описания типа конкретизации и узел описания множества, которому принадлежит эта конкретизация. Таким образом, имеем три вида узлов: узел, представляющий индивида (конкретизацию), который через промежуточные связывающие узлы соединён с узлами типа (Конкр) и множества (Элем). Естественно ввести четвёртый вид: {x| тип} – для произвольного индивида {х} определённого типа (тип).

Профессор х (о котором больше ничего не известно) обозначен {х| проф}. Этот узел соединен с узлом, представляющим множество профессоров, через связывающий узел Элем. С другой стороны, он соединён с узлом, представляющим тип профессора, через связывающий узел Абст. Оператор Абст определяет тип (абстрактный концепт) по описанию какого-либо элемента этого типа. Наконец, можно определить оператор «прототип_для», который можно считать приблизительно обратным оператору Абст. Оператор «прототип_для» (Протот) представляется связывающим узлом, который соединяет тип с описанием этого типа, даваемым «прототипом». Последний позволяет сжато описать мир, разделённый по типам объектов. Описание, даваемое прототипом, можно рассматривать как описание некоторого типичного представителя множества. Следовательно, прототип - разновидность мифической константы. Узел прототипа отличается от узла {x| тип}, который доставляет множество общих свойств объектов одного типа или одного множества. В этом смысле операторы Абст и Протот не являются взаимно обратными.

С абстрактным концептом «профессора университета» связано свойство обладания докторской степенью. С другой стороны, вполне вероятно, что каждый индивид из множества «профессоров университета» имеет докторскую степень. Следовательно, соответствующие иерархии типов и множеств, приведённые на этом рисунке изоморфны (каждому элементу одной системы соответствует один элемент другой системы, а каждой операции в одной системе — операция в другой).

Определение типа посредством рода и различия.

Фраза «Жак посылает книгу Мари». Соответствующая запись её логической формулой такова:

Отправитель (посылка: 8, мужчина: Жак_2)

Получатель(посылка: 8, женщина: Мари_4) Объект(посылка: 8, книга: 22) (6)

В таком представлении каждое значение аргумента типизировано, т.е. ему приписана некая метка типа. Определение типа должно задавать множество необходимых и достаточных условий, характеризующих тот факт, что рассматриваемый объект является объектом типа.

Можно определить метки типов, используя так называемый Аристотелев подход, - через род (genus) в различие (differentia). Тип определяется исходным типом род и высказыванием, называемым различие и отделяющим новый тип от исходного. Например, Посылка – «событие (род), которое происходит, когда два человека, отправитель и получатель, обеспечивают перемещение предмета по почте (различие)». Формально:

Тип Посылка (х) есть (род)

Конкр(х, событие) ^

 (различие)

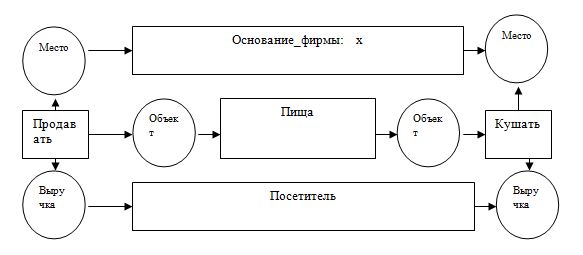
Определение типов можно формализовать с помощью λ-выражений. Пусть t –метка типа, λxF – λ-выражение. Тогда тип t(x) есть F, где тело F этого λ-выражения является различием метки t, а t(x) – её родом. На следующем рисунке приведено определение типа ресторана с использованием концептуального графа.

 

 

---

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Поиск по сайту