Максимум, минимум и экстремумы функции. Необходимое условие существования экстремума.

Приведем точные определения точек экстремума. 

Определение. Точка x₀ называется точкой минимума функции f, если для всех x из некоторой окрестности x₀ выполняется неравенство f(x) ≥ f(x₀. 

Это наглядно показано на рисунке 1: 

 
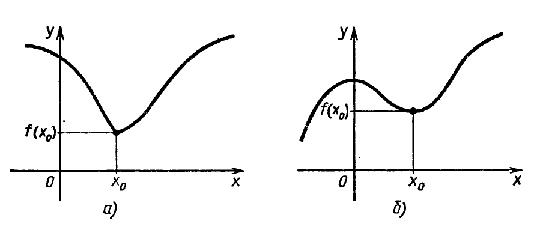
рисунок 1 

Определение. Точка x₀ называется точкой максимума функции f, если для всех x из некоторой окрестности x₀ выполняется неравенство f(x) ≤ f(x₀. 

Это наглядно показано на рисунке 2: 

 
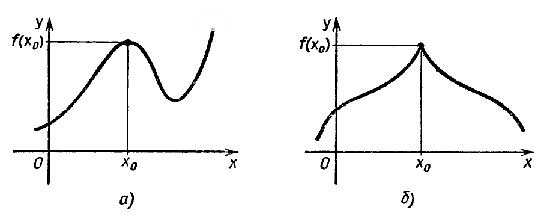
рисунок 2 

По определению значение функции f в точке x₀ является наибольшим среди значений функции в окрестности этой точки, поэтому график функции в окрестности x₀ имеет обычно либо вид гладкого холма, либо вид острого пика (рис. 1 а) и б) соответственно). 

В окрестности точки минимума графики изображаются в виде загругленной или острой впадины (рис. 2 а) и б) соответственно). 

Другие примеры поведения графиков функций в точках максимума и минимума приведены на рисунке ниже: 

 

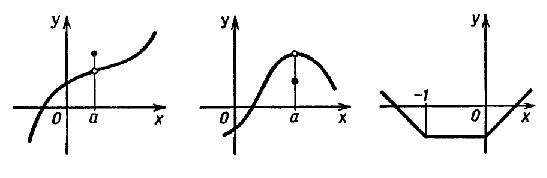
Слева направо: a - точка максимума; a - точка минимума; каждая точка из промежутка [-1; 0] является как точкой максимума, так и точкой минимума. 

Для точек минимума и максимума функции есть общее определение - точки экстремума. Значение функции в этих точках соответственно назывется максимумом или минимумом этой функции. Общее название - экстремум функции. Точки максимума обычно обозначают x_max, а точки минимума - x_min.

Необходимые условия существования экстремумов

• Лемма Ферма. Пусть функция  дифференцируема в точке экстремума x₀. Тогда:

f'(x₀) = 0.

• Если в точке экстремума существует первая частная производная (по какому-либо аргументу), то она равна нулю.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.