Главная » Общенаучные дисциплины » Математика (1 семестр) » Метрическое и нормированное пространства.

Метрическое и нормированное пространства.

Определение метрического пространства

Пусть M — некоторое непустое множество, ρ — некое отображение, ставящие в соответствие двум элементам множества M некоторое вещественное число:

$\rho$ ,

отображение ρ называется метрикой, если оно обладает следующими свойствами (аксиомы метрики):

Аксиома тождества: $~\rho(x,$ ,
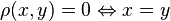Аксиома симметрии: $~\rho(x,$ ,
Аксиома треугольника: $~\rho(x,$ .

Совокупность множества M и определённой на нём метрики ρ называют метрическим пространством и обозначают (M,ρ). Иногда, особенно когда из контекста понятно о какой метрике идёт речь, метрическое пространство обозначают так же, как и само множество М. Элементы метрического пространства обычно называют точками.

Одним из простейших (и важнейших) примеров метрического пространства является числовая прямая. Покажем, что множество вещественных чисел с метрикой ρ(x, y)=|х — у| является метрическим пространством. Действительно, рассмотрим три произвольных вещественных числа

$x,$ ,

Все аксиомы метрического пространства выполняются, по свойствам модуля:

$~|x$ ,

$~|x$ .

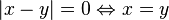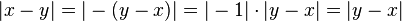Пусть (M, ρ) — метрическое пространство, и A — непустое подмножество множества M, тогда (A, ρ) — тоже является метрическим пространством, которое называетсяподпространством метрического пространства (M,ρ).

Например, множество рациональных чисел является подмножеством действительных чисел:

$\mathbb{Q}$ ,

а следовательно, если взять естественную для вещественных чисел метрику

ρ(x, y) = | x - y |

то

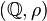
$(\mathbb{Q},\rho)$

будет метрическим пространством.

В принципе, любое множество можно рассматривать как метрическое пространство. Действительно, если для элементов произвольного множества ввести так называемую дискретную метрику:

$\rho(x,$ ,

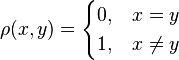то получится метрическое пространство, которое называют пространством изолированных точек.

На одном и том же множестве можно задавать различные метрики (ниже дан пример), однако не следует считать, что метрику можно задавать произвольно. Дело в том, что при решении практических задач метрика, как правило, является частью постановки задачи.

Полунормированным векторным пространством называется пара , где — векторное пространство, а — полунорма в .

Нормированным векторным пространством называется пара , где - векторное пространство, а - норма в .

Часто обозначение и опускают и пишут просто , если из контекста ясно, какая норма или полунорма имеется в виду.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Дисциплины