Главная
»
Общенаучные дисциплины
»
Математика (1 семестр)
»
Декартово произведение множеств. Соответствие и отображение. Эквивалентные множества. Мощность множества. Счетное множество. Множество действительных чисел.
Декартово произведение множеств. Соответствие и отображение. Эквивалентные множества. Мощность множества. Счетное множество. Множество действительных чисел.
- ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ [Cartesian product] — множество А × В всех упорядоченных пар элементов (a, b), из которых a принадлежит множеству A, b — множеству B. Порядок следования пар может быть любым, но расположение элементов в каждой паре (векторе, кортеже) определяется порядком следования перемножаемых элементов. Поэтому A × B ≠ B × A, если B ≠ A.
Если обобщить сказанное на любое количество множеств A1, A2, ..., An, то Д. п.
Если перемножаются одинаковые множества, используется обозначение степени:
An = A × A × A ×...× A
при n сомножителях.
Определение. Взаимно однозначным соответствием между множествами X и Y (или отображением X на Y) называется соответствие (соответственно, отображение), обладающее следующими тремя свойствами: 1) каждому элементу множества Xсоответствует один и только один элемент множества Y; 2) двум различным элементам множества X всегда соответствуют два различных элемента множества Y; 3) всякий элемент множества Y соответствует хотя бы одному элементу множества X.
Заметим, что первые два свойства дают взаимно однозначные отображения X на некоторое подмножество Y. В этом случае говорят о взаимно однозначном отображении X в Y.
Если y = f(x) есть взаимно однозначное отображение X на Y, то каждому можно поставить в соответствие тот единственный элемент, образом которого при отображении f является y. Это соответствие называется обратным отображением для отображения f и обозначается через f -1. В качестве упражнения предлагается доказать, что f -1 есть также взаимно однозначное отображение Y на X и что обратным для отображения f -1 будет исходное отображение f.
Определение. Два множества X и Y, между которыми можно установить взаимно однозначное соответствие, называются равномощными (или эквивалентными), что обозначается символом.
О равномощных множествах говорят также, что они имеют одинаковую мощность. Условимся считать, что пустое множество равномощно только самому себе.
Замечание. Выше мы дали определение понятия равномощности, но не понятие мощности. Можно сказать, что мощность есть то общее, что имеется у всех равномощных между собой множеств. Впрочем, всюду достаточно понятие равномощности.
В теории множеств счётное мно́жество есть бесконечное множество, элементы которого возможно пронумеровать натуральными числами. Более формально: множество Xявляется счётным, если существует биекция  , где
, где 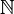 обозначает множество всех натуральных чисел. Другими словами, счётное множество — это множество,равномощное множеству натуральных чисел.
обозначает множество всех натуральных чисел. Другими словами, счётное множество — это множество,равномощное множеству натуральных чисел.
Счётное множество является «наименьшим» бесконечным множеством, то есть в любом бесконечном множестве найдётся счётное подмножество. Мощность множества всех натуральных чисел обозначается символом  (произносится: алеф-нуль).
(произносится: алеф-нуль).
Множество R действительных чисел обладает следующими свойствами.
1. Оно упорядоченное: для любых двух различных чисел α и b имеет место одно из двух соотношений а
2. Множество R плотное: между любыми двумя различными числами a и b содержится бесконечное множество действительных чисел х, т. е. чисел, удовлетворяющих неравенству a<х<b.
Так, если a<b, то одним из них является число (a+b)/2
(a<bÞ 2a<а+b а+b<2bÞ 2а<a+b<2bÞ а<(a+b)/2<b).
3. Множество R непрерывное. Пусть множество R разбито на два непустых класса А и В таких, что каждое действительное число содержится только в одном классе и для каждой пары чисел aєА и bєВ выполнено неравенство a
aєA, bєВ). Оно отделяет числа класса. A от чисел класса В.Число с является либо наибольшим числом в классе А (тогда в классе В нет наименьшего числа), либо наименьшим числом в классе В (тогда в классе А нет наибольшего).
Свойство непрерывности позволяет установить взаимно-однозначное соответствие между множеством всех действительных чисел и множеством всех точек прямой. Это означает, что каждому числу хєR соответствует определенная (единственная) точка числовой оси и, наоборот, каждой точке оси соответствует определенное (единственное) действительное число. Поэтому вместо слова «число» часто говорят «точка».
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.