Главная
»
Общенаучные дисциплины
»
Математика (1 семестр)
»
Предел функции (два определения). Предел функции при стремлении аргумента к бесконечности. Односторонние пределы.Ограниченные функции.
Предел функции (два определения). Предел функции при стремлении аргумента к бесконечности. Односторонние пределы.Ограниченные функции.
Рассмотрим функцию  , определённую на некотором множестве
, определённую на некотором множестве 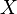 , которое имеет предельную точку
, которое имеет предельную точку 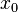 (которая, в свою очередь, не обязана ему принадлежать).
(которая, в свою очередь, не обязана ему принадлежать).
Предел функции по Гейне
Значение  называется пределом (предельным значением) функции
называется пределом (предельным значением) функции  в точке
в точке 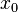 , если для любой последовательности точек
, если для любой последовательности точек 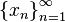 , сходящейся к
, сходящейся к 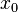 , но не содержащей
, но не содержащей 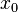 в качестве одного из своих элементов (то есть в проколотой окрестности
в качестве одного из своих элементов (то есть в проколотой окрестности 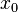 ), последовательность значений функции
), последовательность значений функции  сходится к
сходится к  .
.

Предел функции по Коши
Значение  называется пределом (предельным значением) функции
называется пределом (предельным значением) функции  в точке
в точке 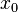 , если для любого наперёд взятого положительного числа
, если для любого наперёд взятого положительного числа  найдётся отвечающее ему положительное число
найдётся отвечающее ему положительное число 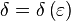 такое, что для всех аргументов
такое, что для всех аргументов  , удовлетворяющих условию
, удовлетворяющих условию 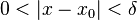 , выполняется неравенство
, выполняется неравенство  .
.
- 0 ~ \exists \delta = \delta \left( \varepsilon \right) ~ \forall x \colon 0 < \left| x - x_0 \right| < \delta \Rightarrow \left| f \left( x \right) - A \right|
Окрестностное определение по Коши
Значение  называется пределом (предельным значением) функции
называется пределом (предельным значением) функции  в точке
в точке 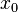 , если для любой окрестности
, если для любой окрестности 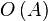 точки
точки  существует выколотая окрестность
существует выколотая окрестность 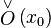 точки
точки 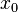 такая, что образ этой окрестности
такая, что образ этой окрестности 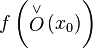 лежит в
лежит в 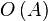 .
.

Если у функции 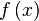 существует предел на бесконечности, равный
существует предел на бесконечности, равный  , то говорят, что функция
, то говорят, что функция 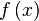 стремится к
стремится к  при стремлении
при стремлении  к бесконечности, и пишут одним из следующих способов:
к бесконечности, и пишут одним из следующих способов:
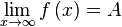 , или
, или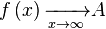 .
.Односторонний предел по Гейне
- Число
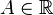 называется правосторонним пределом (правым пределом, пределом справа) функции
называется правосторонним пределом (правым пределом, пределом справа) функции 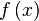 в точке
в точке  , если для всякой последовательности
, если для всякой последовательности 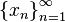 , состоящей из точек, больших числа
, состоящей из точек, больших числа  , которая сама сходится к числу
, которая сама сходится к числу  , соответствующая последовательность значений функции
, соответствующая последовательность значений функции  сходится к числу
сходится к числу  .
.- a \right) \land \lim_{n \to \infty} x_n = a \Rightarrow \lim_{n \to \infty} \left\{ f \left( x_n \right) \right\}_{n = 1}^{\infty} = A
- Число
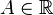 называется левосторонним пределом (левым пределом, пределом слева) функции
называется левосторонним пределом (левым пределом, пределом слева) функции 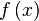 в точке
в точке  , если для всякой последовательности
, если для всякой последовательности 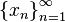 , состоящей из точек, меньших числа
, состоящей из точек, меньших числа  , которая сама сходится к числу
, которая сама сходится к числу  , соответствующая последовательность значений функции
, соответствующая последовательность значений функции  сходится к числу
сходится к числу  .[1]
.[1]
Односторонний предел по Коши
- Число
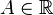 называется правосторонним пределом (правым пределом, пределом справа) функции
называется правосторонним пределом (правым пределом, пределом справа) функции 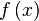 в точке
в точке  , если для всякого положительного числа
, если для всякого положительного числа  отыщется отвечающее ему положительное число
отыщется отвечающее ему положительное число 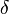 такое, что для всех точек
такое, что для всех точек  из интервала
из интервала 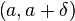 справедливо неравенство
справедливо неравенство  .
.- 0 ~ \exists \delta = \delta \left( \varepsilon \right) > 0 ~ \forall x \in \left( a, a + \delta \right) \colon \left| f \left( x \right) - A \right|
- Число
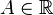 называется левосторонним пределом (левым пределом, пределом слева) функции
называется левосторонним пределом (левым пределом, пределом слева) функции 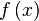 в точке
в точке  , если для всякого положительного числа
, если для всякого положительного числа  отыщется отвечающее ему положительное число
отыщется отвечающее ему положительное число 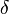 такое, что для всех точек
такое, что для всех точек  из интервала
из интервала 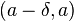 справедливо неравенство
справедливо неравенство  .
.- 0 ~ \exists \delta = \delta \left( \varepsilon \right) > 0 ~ \forall x \in \left( a - \delta, a \right) \colon \left| f \left( x \right) - A \right|
- Для того, чтобы функция f(x) при х®а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие
f(x) = A + a(x),
где a(х) – бесконечно малая при х ® а (a(х)®0 при х ® а).
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.