Если производная некоторой непрерывной функции f(x) на некотором промежутке положительна (f'(x)>0), то на этом промежутке функция возрастает.
Если производная некоторой непрерывной функции f(x) на некотором промежутке отрицательна (f'(x)<0), то на этом промежутке функция убывает.
Эти условия являются достаточными условиями возрастания (убывания функции).
Постараемся понять, почему так происходит (строгое доказательство рассматривается в программе высших учебных заведений). Известно, что геометрический смысл производной - тангенс угла наклона касательной. Значит, если производная положительна, то угол будет острым.
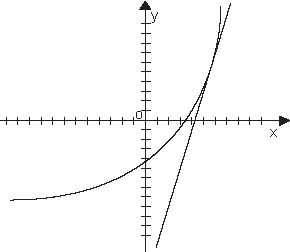
И получается, что график идет «в гору». Если производная отрицательна, то угол наклона будет тупым и получается, что график идет «под гору».
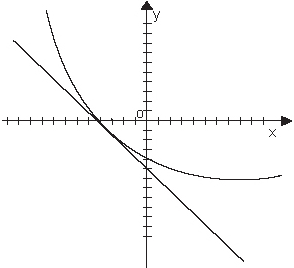
Промежутки возрастания и убывания называют промежутками монотонности функции.
Точка x
0 называется точкой максимума функции f(x), если существует положительное число
E, такое, что для любой точки x из промежутка
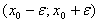
, выполняется неравенство
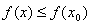
. Иными словами, значение функции f(x
0) самое большое в некоторой окрестности точки x
0.
Точка x
0 называется точкой минимума функции f(x), если существует положительное число
E, такое, что для любой точки x из промежутка
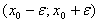
, выполняется неравенство
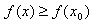
. Иными словами значение функции f(x
0) самое маленькое в некоторой окрестности точки x
0.
На следующем графике точки -9 и 3 являются точками максимума, а точка -2 является точкой минимума.
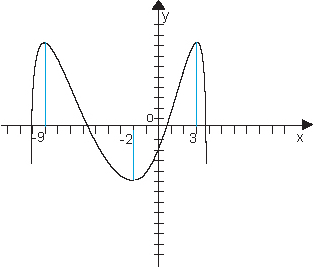
Точки максимума или минимума называются точками экстремума.
Теорема Ферма: Если x
0 - точка экстремума непрерывной функции f(x), то f'(x
0)=0.
Геометрически это выглядит так: в точке экстремума касательная параллельна оси ОХ и, поэтому угол наклона равен 0.
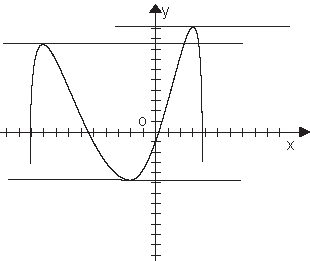
Это условие является необходимым, но не достаточным условием экстремума.