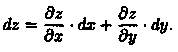Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке x0, а функция g имеет производную в точке y0 = f(x0), то сложная функция h(x) = g(f(x)) также имеет производную в точке x0.
Одномерный случай
Пусть даны функции, определённые в окрестностях на числовой прямой,  где y0 = f(x0), и
где y0 = f(x0), и  Пусть также эти функции дифференцируемы:
Пусть также эти функции дифференцируемы: 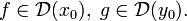 Тогда их композиция также дифференцируема:
Тогда их композиция также дифференцируема: 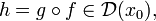 и её производная имеет вид:
и её производная имеет вид:

Замечание
В обозначениях Лейбница цепное правило для вычисления производной функции y = y(x), где x = x(t), принимает следующий вид:

Инвариантность формы первого дифференциала
Дифференциал функции z = g(y) в точке y0 имеет вид:
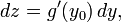
где dy — дифференциал тождественного отображения 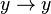 :
:
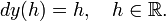
Пусть теперь  Тогда
Тогда 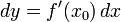 , и согласно цепному правилу:
, и согласно цепному правилу:

Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет.
Пример
Пусть  Тогда функция
Тогда функция  может быть записана в виде композиции
может быть записана в виде композиции 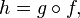 где
где
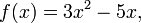
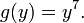
Дифференцируя эти функции отдельно:


получаем

Многомерный случай
Пусть даны функции 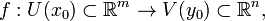 где y0 = f(x0), и
где y0 = f(x0), и 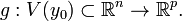 Пусть также эти функции дифференцируемы:
Пусть также эти функции дифференцируемы:  и
и 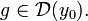 Тогда их композиция тоже дифференцируема, и её дифференциал имеет вид
Тогда их композиция тоже дифференцируема, и её дифференциал имеет вид
- dh(x0) = dg(y0) * df(x0).
В частности, матрица Якоби функции h является произведением матриц Якоби функций g и f:
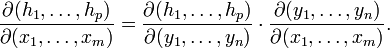
Следствия
- Якобиан композиции двух функций является произведений якобианов индивидуальных функций:

Для частных производных сложной функции справедливо

Инвариантность формы полного дифференциала
Используя правило дифференцирования сложной функции, можно показать, что полный дифференциал обладает свойством инвариантности: полный дифференциал функции z=ƒ(х;у) сохраняет один и тот же вид независимо от того, являются ли аргументы независимыми переменными или функциями независимых переменных.
Пусть z=ƒ(х;у), где х и у — независимые переменные. Тогда полный дифференциал (1-го порядка) функции имеет вид
 (формула (44.5)).
(формула (44.5)).
Рассмотрим сложную функцию z=ƒ(х;у), где х = x(u;v), у = y(u;v), т. е. функцию z = f(x(u;v);y(u;v)) = F(u;v;), где u и v — независимые переменные. Тогда имеем:
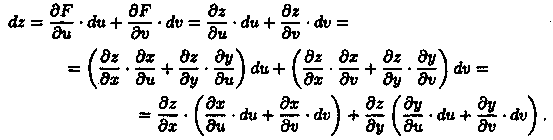
Выражения в скобках представляют собой полные дифференциалы dx и dy функций х = х(u;v) и y = y(u;v). Следовательно, и в этом случае,