Пусть задана функция f(x, y). Тогда каждая из ее частных производных (если они, конечно, существуют) 
и 
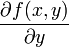, которые называются также частными производными первого порядка, снова являются функцией независимых переменных x, y и может, следовательно также иметь частные производные. Частная производная 
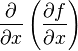обозначается через 
или fxx'', а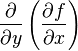 
через 
или fxy''. Таким образом,
, 
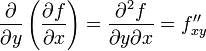
и, аналогично,
, 
.
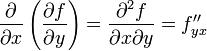Производные fxx'',fxy'',fyx'' и fyy'' называются частными производными второго порядка. Рассматривая частные производные от них, получим всевозможные частные производные третьего порядка: 
,
, 
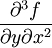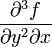и т. д.