Дифференциальные уравнения. Основные понятия. Задачи, приводящие к дифференциальным уравнениям.

Обыкнове́нные дифференциа́льные уравне́ния (ОДУ) — это дифференциальное уравнение вида

где 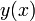 — неизвестная функция (возможно, вектор-функция, тогда 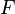, как правило, тоже вектор-функция со значениями в пространстве той же размерности; в этом случае говорят о системе дифференциальных уравнений), зависящая от независимой переменной , штрих означает дифференцирование по . Число 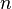 (порядок старшей производной, входящей в данное уравнение) называется порядком дифференциального уравнения (1).

Независимая переменная  часто интерпретируется (особенно в дифференциальных уравнениях, возникающих в физических и других естественно-научных задачах) как время, поэтому её часто обозначают буквой 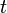. Переменная  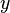— некоторая величина (или совокупность величин, если  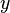является вектор-функцией), изменяющихся со временем. Например,  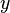может означать набор координат точки в пространстве; в этом случае уравнение (1) описывает движение точки в пространстве, т.е. изменение её координат с течением времени. Независимая переменная  обычно принимает вещественные значения, однако рассматриваются и дифференциальные уравнения, в которых переменная  комплексная (так называемые уравнения с комплексным временем).

Наиболее часто встречаются дифференциальные уравнения вида

в которых старшая производная 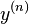 выражается в виде функции от переменных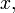   и производных 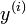 порядков меньше  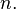Такие дифференциальные уравнения называются нормальными или разрешёнными относительно производной.

В противоположность уравнениям вида (2), дифференциальные уравнения вида (1) называются уравнениями, не разрешёнными относительно производной или неявнымидифференциальными уравнениями.

Классическим решением дифференциального уравнения (2) называется  раз дифференцируемая функция , удовлетворяющая уравнению во всех точках своей области определения. Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительное условие. Начальным условием для уравнения (2) называется условие

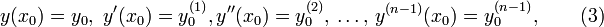
где 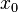 — некоторое фиксированное значение независимой переменной (фиксированный момент времени), а  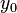и 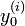 — соответственно, фиксированные значения функции и всех её производных до порядка  включительно. Дифференциальное уравнение (2) вместе с начальным условием (3) называется начальной задачей или задачей Коши:

При достаточно общих ограничениях на функцию , стоящую в правой части уравнения (2), задача Коши для этого уравнение имеет единственное решение, определенное на некотором интервале оси времени , содержащем начальное значение 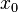 (этот интервал, вообще говоря, может не совпадать со всей осью).

Основные задачи и результаты теории дифференциальных уравнений: существование и единственность решения различных задач для ОДУ, методы решения простейших ОДУ, качественное исследование решений ОДУ без нахождения их явного вида.

Уравнение

F(x, y, y ') = 0,

где y = y(x) — неизвестная, непрерывно дифференцируема на (a,b) функция, называется обыкновенным дифференциальным уравнением первого порядка.

Функция y = y(x) называется решением дифференциального уравнения F(x, y, y ') = 0, если она непрерывно дифференцируема на (a,b) и F(x, y(x), y '(x)) ≡ 0 для всех x из (a,b) .

График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения.

Дифференциальное уравнение 1–го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия.

Задача отыскания решения y = y(x) уравнения F(x, y, y ' ) = 0 , удовлетворяющего условию y(x₀) = y₀, называется задачей Коши (или начальной задачей).

Условие y(x₀) = y₀ — начальное условие.

Любое конкретное решение y = y(x) (решение задачи Коши) уравнения 1–го порядка, называется частным решением уравнения.

Общее решение уравнения, записанное в неявной форме Φ(x, y) = C, называется общим интегралом уравнения.

Частное решение уравнения, записанное в неявной форме Φ(x, y) = 0, называется частным интегралом уравнения.

Уравнение 1-го порядка, разрешенное относительно производной, называют уравнением, записанными в нормальной форме:

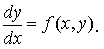
Уравнения первого порядка часто записывают в дифференциальной форме:

M(x, y)dx + N(x, y)dy = 0.

Решение такого уравнения можно искать как в виде y = y(x) , так и в виде x = x(y) .

Огибающие

Допустим, что нам известно для некоторого дифференциального уравнения F(x, у )==0 (1) семейство

F(x, у, С)==0 (2)

интегральных линий, которое покрывает некоторую замкнутую область G плоскости (х, у) так, что через каждую точку такой области проходит по крайней мере одна линия этого семейства. Требуется найти такую проходящую по G линию L, которая в каждой своей точке касается некоторой линии семейства (2) и каждого куска которой касается бесконечное множество линий этого семейства. Такая линия L называется огибающей семейства (2). Очевидно, огибающая семейства интегральных линий будет также интегральной линией уравнения (1), так как в каждой её точке она касается некоторой интегральной кривой и, следовательно, имеет направление поля. Относительно функции F (х, у, С) нам придётся предположить, что она имеет непрерывные производные по всем своим аргументам, и сделать ещё некоторые другие предположения, о которых будет сказано несколько позже и которые в нашем тексте напечатаны курсивом.

Допустим, что искомая линия существует. Так как она в каждой своей точке (х, у) касается некоторой линии  [значок С указывает то значение параметра С, при котором уравнение этой линии получается из общего уравнения (2)], то координаты её точек удовлетворяют уравнению F(x, у, С(х, у)) =0, где теперь С уже не постоянно, но в каждой точке линии L принимает свой значение (именно равное тому С, которое соответствует линии ). Будем рассматривать только такой кусок линии L, где у есть дифференцируемая функция от х (точно так же можно исследовать куски, где х есть дифференцируемая функция от у). Тогда можно считать С в предыдущем уравнении зависящим только от х и переписать это уравнение в следующем виде:

F(x,y, C(x)) = 0. (3)

Допустим, что функция С(х) дифференцируема, не постоянна ни в каком интервале рассматриваемых значений х и нам известна. Найдём тогда из уравнения (3) значение у' для удовлетворяющей этому уравнению функции у от х. Продифференцируем для этого уравнение (3) по х, считая у функцией от х. С другой стороны, если бы мы нашли у' для проходящей через ту же точку (х, у) линии семейства (2), мы получили бы.

Чтобы определяемые из обоих уравнений значения у' (определить у' из этих уравнений можно) были одинаковы (т. е. чтобы в этой точке линия (2) и линия (3) имели общую касательную), необходимо, чтобы было.

Чтобы это произведение было равно 0, надо, чтобы по крайней мере один из его множителей обращался в 0. Если на некотором интервале, это будет означать, что С постоянно, что противоречит предположению. Поэтому для огибающей должно быть (4)

Легко видеть и обратное: именно, что, если при сохранении всех сделанных допущений относительно F(x, у, С) уравнения (3) и (4) определяют у(х) и С(x), как дифференцируемые функции от х, причём С(х) ни в каком интервале рассматриваемых значений х не постоянна, то у = у(х) будет огибающей семейства (2).

Замечание 1. Так как в постановке задачи х и у были совершенно равноправны, то в её решении роли х и у можно поменять.

Замечание 2. Огибающая семейства интегральных линий некоторого дифференциального уравнения 1-го порядка всегда является существенно особой интегральной линией для этого уравнения, так как из каждой её точки по одному направлению выходят по крайней мере две интегральные линии.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.