Дивергенция и ротор векторного поля. Свойства. Формула Стокса и Остроградского.

Пусть X — заданное многообразие, T — касательное расслоение, то есть отображение, которое каждой точке X сопоставляет касательное пространство в данной точке T | _X, тогда сечение касательного расслоения является векторным полем.

Таким образом, векторное поле — это отображение, которое ставит каждой точке многообразия в соответствие вектор из касательного пространства в данной точке.

Частные случаи векторных полей

Векторные поля на прямой

Любую вещественнозначную функцию вещественного переменного можно интерпретировать как одномерное векторное поле.

Векторные поля на плоскости

Если 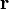 — радиус-вектор, который в заданной системе координат имеет вид 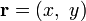, то векторное поле описывается вектор-функцией вида:

Векторные поля в трёхмерном пространстве

Если 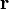 — радиус-вектор, который в заданной системе координат имеет вид 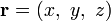, то векторное поле описывается вектор-функцией вида:

В трёхмерном пространстве имеют смысл следующие характеристики векторного поля

Криволинейный интеграл

где точка означает скалярное произведение,  — векторный элемент криволинейного пути, вдоль которого происходит интегрирование, F_τ — проекция 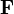 на (положительную) касательную к криволинейному пути, dl — скалярный элемент пути (элемент длины), C — конкретная кривая — путь интегрирования (обычно полагаемая достаточно гладкой). Пожалуй, простейшим физическим прообразом такого интеграла является работа силы 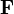, действующей на точку при перемещении точки по заданному пути.

Циркуляция — интеграл по замкнутому контуру:

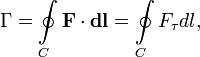
где подынтегральное выражение совпадает с описанным чуть выше, а отличие состоит в пути интегрирования C, который в данном случае по определению замкнут, что обозначается кружком на знаке интеграла.

Поток векторного поля  через поверхность S определяется как интеграл по S:

,

где F_n — проекция вектора поля на нормаль к поверхности, 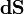 — «векторный элемент поверхности», определяемый, как вектор единичной нормали, умноженный на dS. Простейшим примером этой конструкции является объём жидкости, проходящий через поверхность S, при её течении со скоростью F.

Аналогом производной для векторного поля выступает тензор частных производных (якобиан), который в декартовых координатах имеет вид:

Дивергенция векторного поля — след такого тензора производных. Она не зависит от системы координат (является инвариантом преобразований координат, скаляром), а в прямоугольных декартовых координатах вычисляется по формуле:

Это же выражение можно записать с использованием символического оператора набла

Теорема Остроградского-Гаусса позволяет вычислить поток векторного поля с помощью объёмного интеграла от дивергенции поля.

Ротор — векторная характеристика вихревой составляющей векторного поля. Это вектор с координатами:

,

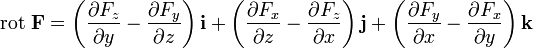где i, j и k — единичные орты для осей x, y и z соответственно.

Для удобства запоминания можно условно представлять ротор как векторное произведение:

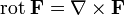
Градиент — важнейшая и простейшая операция, позволяющая получить векторное поле из скалярного поля. Полученное применением такой операции к скалярному полю fвекторное поле называется градиентом f:

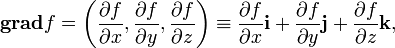
или, записывая с помощью наблы:

Векторное поле, дивергенция которого всюду равна нулю, называется соленоидальным; оно может быть представлено как ротор некоторого другого векторного поля.

Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым); оно может быть представлено как градиент некоторого скалярного поля (потенциала).

Имеет место теорема Гельмгольца: если всюду в области D у векторного поля определены дивергенция и ротор, то это поле может быть представлено в виде суммы потенциального и соленоидального поля.

Векторное поле, у которого и дивергенция, и ротор всюду равны нулю, называется гармоническим; его потенциал представляет собой гармоническую функцию.

Интегральные кривые (силовые линии)

Силовой линией (векторной линией или интегральной кривой, в зависимости от контекста) для поля  называется кривая , касательная к которой во всех точках кривой совпадает со значением поля:

Для силовых полей силовые линии наглядно показывают направление воздействия полевых сил.

Если в достаточно малой области пространства поле нигде не обращается в нуль, то через каждую точку этой области проходит одна и только одна силовая линия. Точки, где вектор поля нулевой — особые, в них направление поля не определено, и поведение силовых линий в окрестности этих точек может быть различным: возможно, через особую точку проходит бесконечно много силовых линий, но возможно, что не проходит ни одна.

Векторное поле называется полным, если его интегральные кривые определены на всём многообразии.

Общая формулировка

Пусть на ориентируемом многообразии M размерности n заданы ориентируемое p-мерное подмногообразие σ и дифференциальная форма ω степени p − 1 класса C¹ (). Тогда, если граница подмногообразия  положительно ориентирована, то

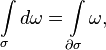
где dω обозначает внешний дифференциал формы ω.

Теорема распространяется на линейные комбинации подмногообразий одной размерности, так называемые цепи. В этом случае формула Стокса реализует двойственность между когомологией де Рама и гомологией циклов многообразия M.

Частные случаи

Формула Ньютона — Лейбница

Пусть дана кривая l, соединяющая две точки a и b (одномерная цепь) в многообразии произвольной размерности. Форма ω нулевой степени класса C¹ — это дифференцируемая функция f. Формула Стокса тогда записывается в виде

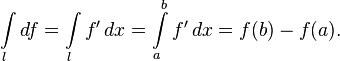
Теорема Грина

Пусть M — плоскость, а D — некоторая её ограниченная область с кусочно-гладкой жордановой границей. Форма первой степени, записанная в координатах x и y — это выражение 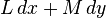, и для интеграла этой формы по границе области D верно

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.