Главная » Общенаучные дисциплины » Математика (2 семестр) » Главная нормаль. Бинормаль. Сопровождающий трехгранник. Кривизна и кручение.

Главная нормаль. Бинормаль. Сопровождающий трехгранник. Кривизна и кручение.

Соприкасающаяся плоскость и нормали

Если взять в качестве $m$ плоскость, проходящую через точку $O$ кривой $M$ , то условие соприкосновения при $\alpha$ определяет соприкасающуюся плоскость кривой (рис. 1). Дважды дифференцируемая кривая в каждой точке имеет соприкасающуюся плоскость. Она либо единственная, либо любая плоскость, проходящая через касательную кривой, является соприкасающейся.

Пусть $\mathbf{r}$ — уравнение кривой. Тогда уравнение $\mathbf{R}$ её соприкасающейся плоскости определяется из соотношения:

$(\mathbf{R}$

В координатах оно имеет вид:

$\begin{vmatrix}$

Прямая, перпендикулярная касательной и проходящая через точку касания, называется нормалью к кривой. Плоскость, перпендикулярная касательной в данной точке кривой, называется нормальной плоскостью; все нормали для данной точки лежат в нормальной плоскости. Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью, а нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью. Также нормалью и бинормалью для краткости могут называть единичные векторы вдоль этих прямых (при этом направление вектора главной нормали обычно выбирают совпадающим с направлением вектора кривизны кривой).

Векторное уравнение бинормали в точке, отвечающей значению $t 0$ параметра $t$ , имеет вид:

$\boldsymbol{r}(\lambda)=\boldsymbol{r}(t_0)+\lambda$

Направление главной нормали может быть получено как двойное векторное произведение: $[\mathbf{r}'$ .

Для плоской кривой содержащая её плоскость совпадает с соприкасающейся. Нормаль, с точностью до знака, только одна — главная, и её уравнение в точке $(x_0,\$ имеет следующий вид.

Параметрическое задание: $Y$
Явное задание: $Y$
Неявное задание: $Y$
Кривизна
При движении вдоль кривой её касательная меняет направление. Скорость этого вращения (отношение угла поворота касательной за бесконечно малый промежуток времени к этому промежутку) при равномерном, с единичной скоростью, движении вдоль кривой называется кривизной кривой. Производная же по времени положительного единичного вектора касательной называется в этом случае вектором кривизны кривой. То и другое - функции точки кривой. Кривизна есть абсолютная величина вектора кривизны.
В случае произвольного параметрического задания кривой кривизна кривой в трехмерном пространстве определяется по формуле
$k_1$ ,
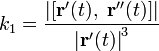где 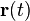$\mathbf{r}(t)$ — вектор-функция с координатами $x(t),\$ .
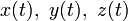В координатах:
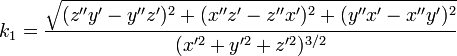
$k_1=\frac{\sqrt{(z''y'-y''z')^2+(x''z'-z''x')^2+(y''x'-x''y')^2}}{(x'^2+y'^2+z'^2)^{3/2}}$
Для кривой в более многомерном пространстве можно заменить векторное произведение, обозначенное здесь квадратными скобками, на внешнее произведение.
Также для кривой в любой размерности пространства можно воспользоваться формулой вектора кривизны:
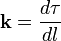
$\mathbf$
и фактом, что кривизна есть его модуль, а также выражением для единичного вектора касательной
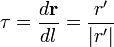
$\mathbf$
и
$dl$
и получить для кривизны формулу:
$k$
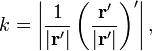
или, раскрыв скобки:
$k$

Прямые и только прямые имеют всюду равную нулю кривизну. Поэтому кривизна наглядно показывает, насколько (в данной точке) кривая отличается от прямой линии: чем ближе кривизна к нулю, тем это отличие меньше. Кривизна окружности радиуса $R$ равна $1 / R$ .
Дважды дифференцируемая кривая в каждой точке, где кривизна отлична от нуля, имеет единственную соприкасающуюся плоскость.
Для плоских кривых можно различать направление вращения касательной при движении вдоль кривой, поэтому кривизне можно приписывать знак в зависимости от направления этого вращения. Кривизна плоской кривой, задаваемой уравнениями 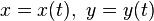$x=x(t),\$ , определяется по формуле
$k=$ .
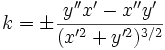Знак $+$ или $-$ берётся по соглашению, но сохраняется вдоль всей кривой.
Кручение
При движении вдоль кривой в окрестности заданной точки соприкасающаяся плоскость вращается, причём касательная к кривой является мгновенной осью этого вращения. Скорость вращения соприкасающейся плоскости при равномерном, с единичной скоростью, движении называется кручением. Направление вращения определяет знак кручения.
Трижды дифференцируемая кривая в каждой точке с отличной от нуля кривизной имеет определённое кручение. В случае параметрического задания кривой уравнениями (1) кручение кривой определяется по формуле
$k_2$
здесь $( * , * , * )$ обозначает смешанное произведение. В координатах для натуральной параметризации:
$k_2$
Для прямой кручение не определено, поскольку неоднозначно определяется соприкасающаяся плоскость. Плоская кривая в каждой точке имеет кручение, равное нулю. Обратно, кривая с тождественно равным нулю кручением — плоская.