Главная » Общенаучные дисциплины » Математика (2 семестр) » Криволинейный интеграл 1-го рода. Свойства. Вычисление

Криволинейный интеграл 1-го рода. Свойства. Вычисление

Криволинейный интеграл первого рода

Свойства

1. Линейность:

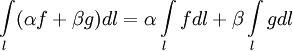
$~\int\limits_l(\alpha$

2. Аддитивность: если 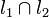$l_1\cap$ в одной точке, то

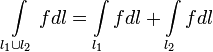
$\int\limits_{l_1\cup$

3. Монотонность: если 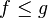$f$ на $l$ , то

$\int\limits_l$

4. Теорема о среднем для непрерывной вдоль $l$ функции $f$ :

$\exists$

Очевидно, что: 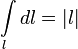$\int\limits_{l}{d}l=\left|$ .

5. Изменение направления обхода кривой интегрирования не влияет на знак интеграла: 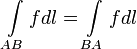$\int\limits_{AB}{f}dl=\int\limits_{BA}{f}dl$ .

6. Криволинейный интеграл первого рода не зависит от параметризации кривой.

Вычисление

Пусть $l$ — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция 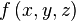$f\left($ определена и интегрируема вдоль кривой $l$ в смысле криволинейного интеграла первого рода. Тогда

$\int\limits_{l}{f\left($ .

Здесь точкой обозначена производная по $t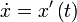$ : $\dot{x}={x}'\left($ .

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Дисциплины