Главная » Общенаучные дисциплины » Математика (2 семестр) » Криволинейный интеграл 2-го рода. Свойства. Вычисление

Криволинейный интеграл 2-го рода. Свойства. Вычисление

Криволинейный интеграл второго рода

Свойства

1. Линейность:

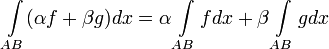
$\int\limits_{AB}(\alpha$

2. Аддитивность:

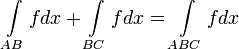
$\int\limits_{AB}fdx$

3. Монотонность: если 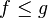$f$ на $Γ$ , то

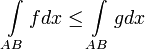
$\int\limits_{AB}fdx$

4. Оценка модуля:

$|\int\limits_{AB}f(x)dx|$

5. Теорема о среднем: если $f$ непрерывна на $Γ$ , то 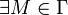$\exists$ , такая что: $\int\limits_{AB}f(x)dx$
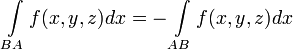
6. $\int\limits_{BA}f(x,y,z)dx$

Вычисление

Пусть $l$ — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция 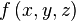$f\left($ определена и интегрируема вдоль кривой $l$ в смысле криволинейного интеграла второго рода. Тогда

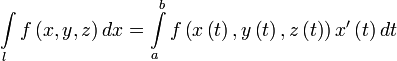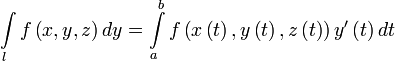$\int\limits_{l}{f\left($ ,

$\int\limits_{l}{f\left($ .

Если обозначить за 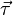${\vec{\tau$ касательный вектор к кривой $l$ , то нетрудно показать, что

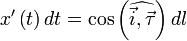
${x}'\left($

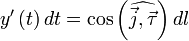
${y}'\left($

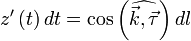
${z}'\left($

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Дисциплины