Главная
»
Общенаучные дисциплины
»
Математика (2 семестр)
»
Оператор Гамильтона. Некоторые его применения.
Оператор Гамильтона. Некоторые его применения.
Опера́тор на́бла (оператор Гамильтона) — векторный дифференциальный оператор, обозначаемый символом  (набла) (в Юникоде
(набла) (в Юникоде U+2207, ∇). Для трёхмерного евклидова пространства в прямоугольных декартовых координатах оператор набла определяется следующим образом:
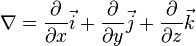 ,
,
где 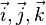 — единичные векторы по осям x, y, z.
— единичные векторы по осям x, y, z.
Через оператор набла естественным способом выражаются основные операции векторного анализа: grad (градиент), div (дивергенция), rot (ротор), а также оператор Лапласа (см. ниже). Широко употребляется в описанном смысле в физике и математике (хотя иногда графический символ  используется также для обозначения некоторых других, хотя в некотором отношении не совсем далеких от рассмотренного, математических объектов, например, ковариантной производной).
используется также для обозначения некоторых других, хотя в некотором отношении не совсем далеких от рассмотренного, математических объектов, например, ковариантной производной).
Под n-мерным оператором набла подразумевается вектор с компонентами  в n-мерном пространстве.
в n-мерном пространстве.
Иногда, особенно при начертании от руки, над оператором набла рисуют стрелку:  — чтобы подчеркнуть векторный характер оператора. Смысл такого начертания ничем не отличается от обычного
— чтобы подчеркнуть векторный характер оператора. Смысл такого начертания ничем не отличается от обычного  .
.
- Иногда (особенно когда речь идет только о применении к скалярным функциям), оператор набла называют оператором градиента, каковым он в применении к скалярным функциям (полям) и является.
- Замечание: в физике в наше время название оператор Гамильтона по отношению к оператору набла стараются не употреблять, особенно в квантовой физике, во избежание путаницы с квантовым гамильтонианом, имеющим, в отличие от классического, операторную природу.
Свойства оператора набла
Этот вектор приобретает смысл в сочетании со скалярной или векторной функцией, к которой он применяется.
Если умножить вектор  на скаляр φ, то получится вектор
на скаляр φ, то получится вектор
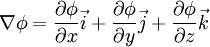 ,
,
который представляет собой градиент функции φ.
Если вектор  скалярно умножить на вектор
скалярно умножить на вектор  , получится скаляр
, получится скаляр
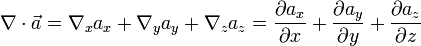 ,
,
то есть дивергенция вектора  .
.
Если  умножить на
умножить на  векторно, то получится ротор вектора
векторно, то получится ротор вектора  :
:
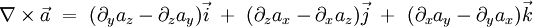
- Замечание: как и для обозначения скалярного и векторного произведения вообще, в случае их применения с оператором набла, наряду с использоваными выше, часто используются эквивалентные им альтернативные обозначения, так, например, вместо
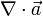 нередко пишут
нередко пишут  , а вместо
, а вместо 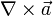 пишут
пишут  ; это касается и формул, приводимых ниже.
; это касается и формул, приводимых ниже.
Соответственно, скалярное произведение 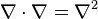 есть скалярный оператор, называемый оператором Лапласа. Последний обозначается также
есть скалярный оператор, называемый оператором Лапласа. Последний обозначается также 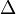 . В декартовых координатах оператор Лапласа определяется следующим образом:
. В декартовых координатах оператор Лапласа определяется следующим образом:
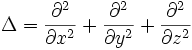 .
.
Поскольку оператор набла является дифференциальным оператором, то при преобразовании выражений необходимо учитывать как правила векторной алгебры, так и правила дифференцирования. Например:
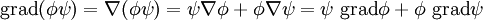
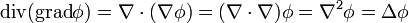
То есть производная выражения, зависящего от двух полей, есть сумма выражений, в каждом из которых дифференцированию подвергается только одно поле.
Для удобства обозначения того, на какие поля действует набла, принято считать, что в произведении полей и операторов каждый оператор действует на выражение, стоящее справа от него, и не действует на всё, что стоит слева. Если требуется, чтобы оператор действовал на поле, стоящее слева, это поле каким-то образом отмечают, например, ставя над буквой стрелочку:
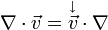
Такая форма записи обычно используется в промежуточных преобразованиях. Из-за её неудобства в окончательном ответе от стрелочек стараются избавиться.
Операторы второго порядка
Так как существуют различные способы перемножения векторов и скаляров, с помощью оператора набла можно записать различные виды дифференцирования. Комбинирование скалярных и векторных произведений даёт 7 различных вариантов производных второго порядка:
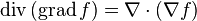
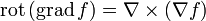
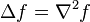
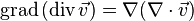

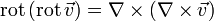

Для достаточно гладких полей (дважды непрерывно дифференцируемых) эти операторы не независимы. Два из них всегда равны нулю:
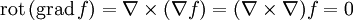

Два всегда совпадают:
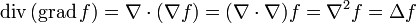
Три оставшихся связаны соотношением:
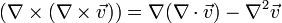
Еще одно может быть выражено через тензорное произведение векторов:
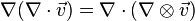
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.