Главная » Общенаучные дисциплины » Математика (2 семестр) » Понятие и представление комплексных чисел

Понятие и представление комплексных чисел

Алгебраическая форма комплексного числа. Аргумент и модуль комплексного числа.

Определение 1: Комплексным числом называется пара действительных чисел (x,y). Причем комплексное число z = x + i*y, где i - мнимая единица. Данное определение и задает представление комплексного числа в алгебраической форме. Введем ещё несколько определений, в частности поясним понятие аргумента и модуля комплексного числа.

Определение 2: Аргументом комплексного числа называется значение угла arg(z)=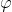 $\varphi$ . Главное значение аргумента находится на отрезке от минус 180 до 180.

Определение 3: Модулем комплексного числа называется число 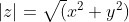$|z|$ .

Геометрической интерпретацией модуля комплексного числа является длина вектора 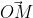$\vec{OM}$ . А аргумент комплексного числа - это угол отклонения данного вектора от положительного направления оси абсцисс, т.е. $arg(z)$ .

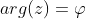Тригонометрическая форма комплексного числа. Формула Муавра

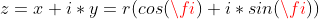$z$ слева у нас алгебраическая форма числа, справа тригонометрическая форма числа.

r - модуль комплексного числа z.

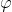$\varphi$ - главный аргумент комплексного числа z.

Теорема 1: Модуль произведения двух комплексных чисел равен произведению модулей этих чисел, а аргумент произведения двух комплексных чисел равен сумме модулей, т.е. 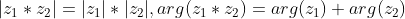$|z_{1}*z_{2}|$ .

Теорема легко доказывается, если мы возьмем два комплексных числа в тригонометрической форме и перемножим их между собой и результат снова представим в тригонометрической форме.

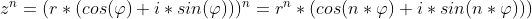$z^{n}$ - это и естьформула Муавра

Как видно из формулы Муавра результат возведения в степень комплексного числа однозначный. Что нельзя сказать про взятия корня из комплексного числа.

Теорема 2: Корень n-ой степени из ненулевого комплексного числа имеет n-значений, которые лежат на окружности радиуса $\sqrt[n]{r}$ и делят её на n равных частей и могут быть найдены по следующей формуле:

$u$

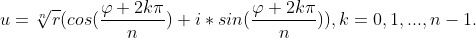
Замечание 1: Значение параметра k не обязательно брать от 0 до n - 1, нужно брать любые n подряд идущих целых числа.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Дисциплины