Главная » Общенаучные дисциплины » Математика (2 семестр) » Приближенное решение дифференциальных уравнений первого порядка методом Эйлера.

Приближенное решение дифференциальных уравнений первого порядка методом Эйлера.

Пусть дана задача Коши для уравнения первого порядка

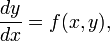
$\frac{dy}{dx}=f(x,y),$

$y_{|_{x=x_0}}=y_0,$

где функция $f$ определена на некоторой области 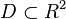$D\subset$ . Решение разыскивается на интервале $[x 0, b)$ . На этом интервале введем узлы

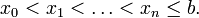
$x_0<x_1<\dots<x_n\le$

Приближенное решение в узлах $x i$ , которое обозначим через $y i$ определяется по формуле

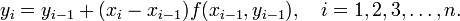
$y_i=y_{i-1}+(x_i-x_{i-1})f(x_{i-1},y_{i-1}),\quad$

Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.

Оценка погрешности

Метод Эйлера является методом первого порядка. Если функция $f$ непрерывна в $D$ и непрерывно дифференцируема по переменной $y$ в $D$ , то имеет место следующая оценка погрешности

$\left|y(x_i)-y_i\right|=O(h),$

где $h$ — средний шаг, то есть существует $C > 0$ такая, что $C^{-1}\le$ .

Заметим, что условия гладкости на правую часть, гарантирующие единственность решения задачи Коши, необходимы для обоснования сходимости метода Эйлера.

Значение метода Эйлера

Метод Эйлера являлся исторически первым методом численного решения задачи Коши. О. Коши использовал этот метод для доказательства существования решения задачи Коши. Ввиду невысокой точности и вычислительной неустойчивости для практического нахождения решений задачи Коши метод Эйлера применяется редко. Однако в виду своей простоты метод Эйлера находит свое применение в теоретических исследованиях дифференциальных уравнений, задач вариационного исчисления и ряда других математических проблем.

Модифицированный метод Эйлера с пересчетом

Вычисления по методу Эйлера с пересчетом делаются в два этапа.

Прогноз:

$\tilde$ .

Коррекция:

$y_i=y_{i-1}+\frac{(x_i-x_{i-1})}{2}(f(x_{i-1},y_{i-1})+f(x_i,\tilde$ .

Модифицированный метод Эйлера с пересчетом имеет второй порядок точности, однако для его реализации необходимо дважды вычислять правую часть функции. Заметим, что метод Эйлера с пересчетом представляет собой разновидность методов Рунге-Кутта (предиктор-корректор).

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Дисциплины