Условный экстремум. Множитель Лагранжа. Необходимое условие существования условного экстремума. Достаточное условиесуществования условного экстремума

Пусть  - открытое множество и на G заданы функции 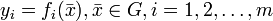. Обозначим  такую, что

 - уравнение связи.

Определение

Пусть на G определена функция 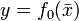. Точка  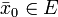называется точкой условного экстремума функции  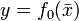относительно уравнений связи, если она является точкой обычного экстремума  на множестве E ( рассматриваются окрестности  ).

Метод множителей Лагранжа для решения задачи условного экстремума

Теорема

Пусть 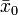 - точка условного экстремума функции  при выполнении уравнений связи. Тогда в этой точке 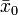 градиенты  являются линейно зависимыми, то есть 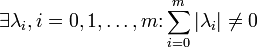 но \sum^{m}_{i=0}.

Следствие

Если 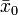 - точка условного экстремума функции  относительно уравнений связи, то 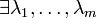 такие, что в точке  или в координатном виде .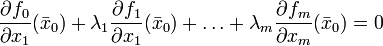

Достаточное условие условного экстремума

Пусть 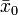 является стационарной точкой функции Лагранжа  при 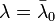. Если  - отрицательно (положительно) определена квадратическая форма переменных 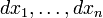 при условии , то 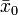 является точкой max (min для положительно определенной) условного экстремума. Если она за этих условий не является знакоопределенной, тогда экстремума нет.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.