Главная
»
Общенаучные дисциплины
»
Математика (2 семестр)
»
Векторное поле. Поток поля. Циркуляция.
Векторное поле. Поток поля. Циркуляция.
Векторные поля
К простейшим векторным полям относятся: соленоидальное, потенциальное игармоническое.
Определение 1: Векторное поле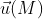 называется соленоидальным или трубчатым, если во всех точках поля
называется соленоидальным или трубчатым, если во всех точках поля 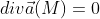
Соленоидальное поле не имеет ни источников, ни стоков, его векторные линии замкнуты. Поскольку div\vec{B}=0, то поле вектора магнитной индукции является соленоидальным.
Определение 2: Векторное поле 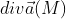 называется потенциальным илибезвихревым, если во всех точках поля
называется потенциальным илибезвихревым, если во всех точках поля 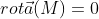
Для потенциального векторного поля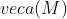 всегда найдется такая скалярная функция u(M) (потенциал векторного поля
всегда найдется такая скалярная функция u(M) (потенциал векторного поля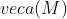 ), что
), что 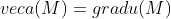 .
.
Потенциал векторного поля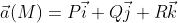 можно найти по формуле
можно найти по формуле
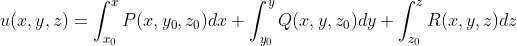
где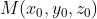 – произвольная точка поля, в которой функции P, Q, R определены, С – произвольная постоянная.
– произвольная точка поля, в которой функции P, Q, R определены, С – произвольная постоянная.
Определение 3: Векторное поле называется гармоническим, если во всех точках поля 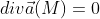 и
и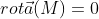
и
т.е. поле является соленоидальным и потенциальным.
Потенциал u гармонического поля удовлетворяет уравнению Лапласа
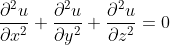
Циркуляция векторного поля
Рассмотрим непрерывное векторное поле 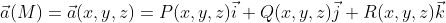 определённое в каждой точке гладкой замкнутой кривой L.
определённое в каждой точке гладкой замкнутой кривой L.
Определение 4: Циркуляцией С векторного поля 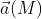 вдоль замкнутой кривой L называется криволинейный интеграл второго рода
вдоль замкнутой кривой L называется криволинейный интеграл второго рода
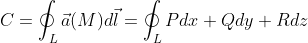
В случае, когда векторное поле 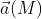 является силовым полем, циркуляция даёт величину работы этого поля вдоль кривой L .
является силовым полем, циркуляция даёт величину работы этого поля вдоль кривой L .
Если кривая L лежит в плоскости xOy, то направление обхода против часовой стрелки считается положительным, а по часовой – отрицательным.
Примеры циркуляций векторных полей:
1. Циркуляция вектора напряженности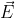 электрического поля вдоль контура L равна э.д.с., возникающей в этом контуре
электрического поля вдоль контура L равна э.д.с., возникающей в этом контуре 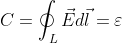
2. Циркуляция вектора напряженности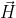 магнитного поля вдоль контура L равна силе тока в этом контуре {tex}C = \oint_{L}\vec{H}d\vec{l} = i{/thttp://naotlichno.by/administrator/index.php?option=com_content§ionid=0&task=edit&cid[]=22ex}
магнитного поля вдоль контура L равна силе тока в этом контуре {tex}C = \oint_{L}\vec{H}d\vec{l} = i{/thttp://naotlichno.by/administrator/index.php?option=com_content§ionid=0&task=edit&cid[]=22ex}
Понятие о поверхностных интегралах.
Поток векторного поля
Пусть в каждой точке некоторой поверхности S определен непрерывный вектор 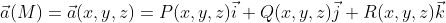
Зададим направление нормали 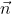 к поверхности S (эту сторону поверхности считаем положительной). Проекция
к поверхности S (эту сторону поверхности считаем положительной). Проекция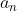 вектора
вектора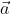 в каждой точке M поверхности S будет являться скаляром. Поэтому функция
в каждой точке M поверхности S будет являться скаляром. Поэтому функция 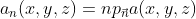 будет скалярной функцией и от нее можно вычислить поверхностный интеграл первого рода.
будет скалярной функцией и от нее можно вычислить поверхностный интеграл первого рода.
Определение 5: Поверхностным интегралом второго рода от вектора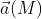 по поверхности S называется поверхностный интеграл первого рода от проекции
по поверхности S называется поверхностный интеграл первого рода от проекции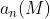 этого вектора на вектор нормали n к S и обозначается
этого вектора на вектор нормали n к S и обозначается
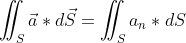
В теории поля поверхностный интеграл второго рода называется потоком векторного поля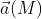 через поверхность.
через поверхность.
Примеры потоков векторных полей
1) Поток электрического поля точечного заряда напряженностью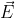 через замкнутую поверхность S, охватывающую этот заряд, равен
через замкнутую поверхность S, охватывающую этот заряд, равен
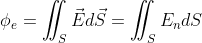 .
.
2) Поток магнитного поля с индукцией 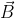 через поверхность S равен
через поверхность S равен
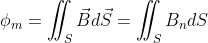
Из этой статьи Вы узнали:
- основные вида простейших векторных полей: соленоидальное, потенциальноеи гармоническое
- способы определения вида векторного поля
- циркуляцию векторного поля и формулу подсчета циркуляции
- поток векторного поля и формулу подсчета потока векторного поля
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.