Комплексные числа. Предел последовательности.Ряды комплексных чисел. Функция комплексной переменной. Предел инепрырывность функции.

1. Предел последовательности комплексных чисел. Расширенная комплексная плоскость. Числовые ряды

Функции комплексного переменного

1) 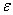-окрестностью точки  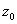будем называть множество точек  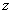комплексной плоскости, удовлетво-ряющих условию:  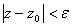-- открытый круг с центром в точке  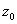радиуса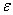 

2) Пусть дана последовательность 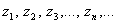 Будем называть  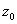пределом последовательности, если выполняется: 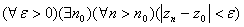. Тогда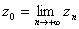 

Теорема1: последовательность 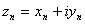 имеет предел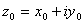  

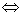
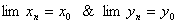
1) 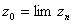. Доказать, что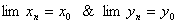 

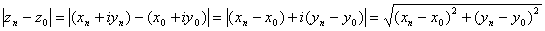
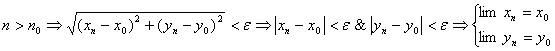
2) 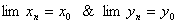. Тогда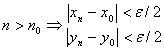 

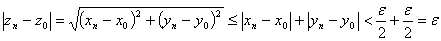
Теорема2: критерий Коши 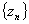 -- сходится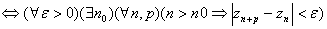 

3) Последовательность 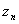 называется ограниченной, если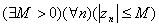 

Теорема3 (Б-В): из всякой ограниченной бесконечной последовательности можно выделить сходящуюся подпоследовательность

4) Будем говорить, что 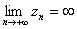, если 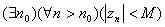. Окрестностью бесконечно удалённой точки будем называть внешность любого круга с центром в н/к достаточно большого радиуса

5) Комплексная плоскость с 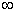-удалённой точкой -- расширенная комплексная плоскость

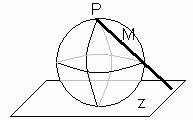Это сфера Римана (стереографическая проекция)

2. Понятие функции комплексной переменного. Предел. Непрерывность

1) Область -- множество точек комплексной плоскости, удовлетворяющих следующим двум условиям:

            1) Все точки этого множества внутренние

            2) Любые 2 точки этого множества можно соединить ломаной, лежащей в этой области

Область будем обозначать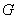 

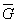 -- область с границей, замкнутая область

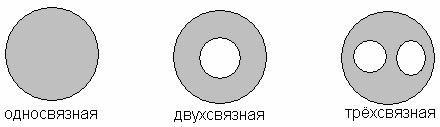
2) Область 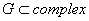 называется односвязной, если она удовлетворяет следующему условию: какую бы замкнутую непрерывную кривую в этой области мы не взяли, часть плоскости, внутренняя по отношению кривой, такжу принадлежит этой области

Проще говоря, односвязная область -- область без дыр

3) На комплексной плоскости задана функция 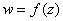, если указано правило, по которому каждому  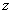ставится одно или несколько значений 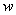. В первом случае функция  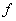однозначная, во втором -- многозначная

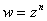 -- однозначная

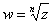 -- многозначная (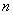-значная)

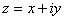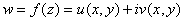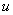Поскольку , то ,  и 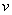 -- вещественные функции: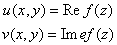 

4) 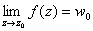, если выполняется условие: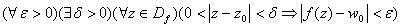 

5) Функция 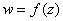называется непрерывной в точке 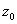, есл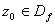и  и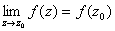 

Непрерывность в области означает непрерывность в каждой точке области

6) 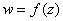 называется равномерно непрерывной в области , если выполняется следующее условие: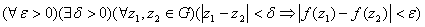 

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.