Функциональные и степенные ряды

Равномерносходящиеся функциональные ряды

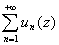 -- функциональный ряд, где  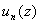-- функции, заданные на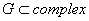 

Если фиксировать 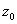, то получим  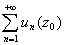-- числовой ряд. Если он сходится, то  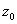-- точка сходимости данного функционального ряда

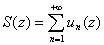 -- сумма ряда. Если ряд равномерно сходится, то  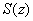будет непрерывной

1) 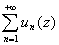 -- равномерно сходящийся к своей предельной функции  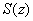на 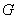, если выполняется следующее условие: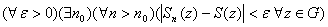 

Теорема6: пусть члены функционального ряда 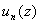 есть функции непрерывные на множестве  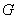и данный ряд равномерно сходится на этом множестве, тогда сумма этого ряда есть функция, непрерывная на множестве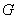 

Возьмём 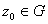. Тогда:

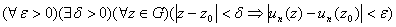 -- непрерывность функций

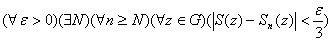 -- равномерная сходимость

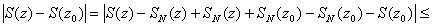
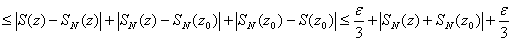
Так как 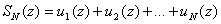, то она непрерывна как сумма конечного числа непрерывных функций. Тогда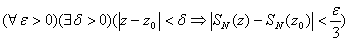 

Теорема7 (критерий Коши для равномерной сходимости функциональных рядов):  чтобы 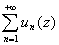 равномерно сходился на , 

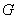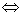
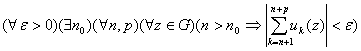
Теорема8 (признак Вейерштрасса)

Пусть 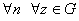 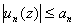       и 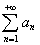-- сходится

Тогда 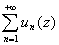 равномерно сходится на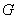 

Сравнивать комплексные числа мы не можем, поэтому нет признаков Абеля и Дирихле)

7. Степенные ряды. Теорема Адамара

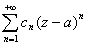 -- степенной ряд

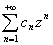 -- степенной ряд

При 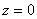 любой степенной ряд сходится

Теорема9 (Абеля): пусть 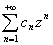 -- сходится в точке 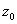, тогда данный ряд сходится в любой точке, что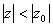 

Доказательство: пусть 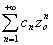 -- сходится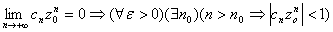 

Пусть теперь 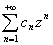. Тогда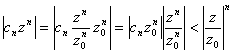 

Пусть 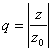, причём 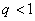, тогда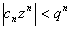 

Ряд 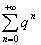 -- сходится как геометрическая прогрессия с показателем меньше 1. Тогда по признаку сравнения наш ряд сходится

Следствие: для 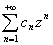 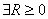, что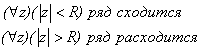 

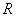 -- радиус сходимости степенного ряда.  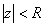-- круг сходимости степенного ряда

Теорема10 (Коши-Адамара): рассмотрим степенной ряд 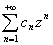, тогда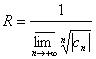 

Пусть 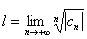, тогда можно рассмотреть 3 случая: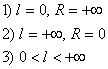 

Во всех трёх случаях надо доказать, что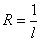 

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.