Производная функции. Условия Коши-Римана. Аналитические функции. Конфорное отображение. Геометрический смысларгумента и модуля производной аналитической функции.

Понятие аналитической функции. Условия Коши-Римана

1) Производной функции 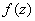 в точке  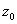мы будем называть предел отношения вида: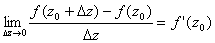 

2) Функция называется дифференцируемой в точке 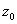, если у неё в этой точке существует конечная производная. Учитываются все пути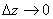 

Теорема4 (условие Коши-Римана): пусть 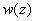 -- дифференцируема в точке 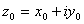, причём 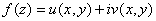. Тогда функци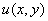и  и 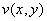 в точке  имеют частные производные, причём  и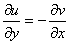 

Теорема5: пусть дана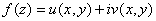 

Пусть 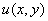 и 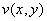 -- дифференцируемы в точке , и в этой области выполняется условие Коши-Римана. Тогда 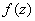 -- дифференцируема в точке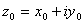 

3) 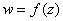 называется дифференцируемой в области, если она дифференцируема в каждой точке этой области

4) Функция называется аналитичной в области 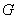, если она дифференцируема в области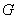 

Понятие аналитичности функции относится к области, но бы и про конкретную точку будем говорить, что функция аналитична в этой точке, имея ввиду аналитичность в окрестности этой точки

4. Сопряжённые гармонические функции

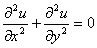 -- уравнение Лапласа

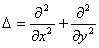 -- оператор Лапласа

1) Функцию 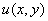, удовлетворяющую уравнению Лапласа, мы будем называть гармонической функцией

Действительная часть аналитической функции есть функция гармоническая:

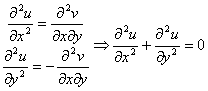
Аналогично можно показать, что мнимая часть аналитической функции есть функция гармоническая

2) Две гармонические функции, удовлетворяющие условиям Коши-Римана, мы будем называть сопряжёнными гармоническими функциями

5. Геометрический смысл модуля и аргумента производной

Пусть 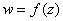 -- аналитична в области 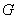. Возьмём точку  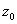из области  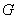и потребуем, чтобы  (так как у нуля аргумент не определён)

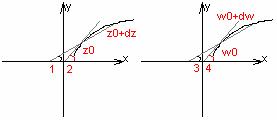
тттттт

1) Отображение, обладающее 2 свойствами: консерватизмом углов и постоянством растяжений, мы будем называть конформным отображением

При этом если углы сохраняются по направлению, то конформное отображение -- отображение 1 рода, а если меняются на противоположные, то 2 рода. Таким образом, отображение, задаваемое аналитической функцией в тех точках, где производная 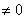, есть конформное отображение 1 рода

Конформное преобразование (математическое), отображение одной фигуры (области) на другую, при котором две любые кривые, пересекающиеся под некоторым углом во внутренней точке первой фигуры, преобразуются в кривые второй фигуры, пересекающиеся под тем же углом.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.