Главная
»
Общенаучные дисциплины
»
Математика (3 семестр)
»
Интегральная теорема Коши.
Интегральная теорема Коши.
Интегральная формула Коши
Теорема16: пусть 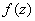 -- аналитична в односвязной области
-- аналитична в односвязной области 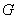 , охватываемой контуром
, охватываемой контуром 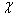 , и на самом
, и на самом 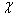 . Тогда для любой точки
. Тогда для любой точки 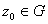 справедливо:
справедливо: 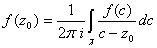 -- формула связывает внутренние значения со значениями на контуре
-- формула связывает внутренние значения со значениями на контуре
Доказательство длинное и сложное
разобрать примеры
Интегральная формула Коши для сложного контура
Теорема17: пусть 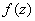 -- аналитична в многосвязной области
-- аналитична в многосвязной области 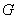 , ограниченной сложным контуром
, ограниченной сложным контуром 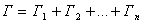 , и на самом этом контуре. Тогда
, и на самом этом контуре. Тогда 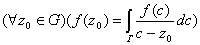
Доказательство с помощью разбиения на односвязные области и теоремы16 (легко)
Интеграл типа Коши
Пусть 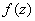 -- непрерывна на
-- непрерывна на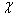 . Рассмотрим функцию
. Рассмотрим функцию 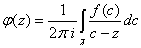 . Понятно, что если
. Понятно, что если 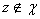 , то подынтегральная функция
, то подынтегральная функция 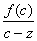 -- непрерывна на кривой
-- непрерывна на кривой 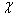
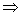
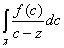 -- всегда существует
-- всегда существует
Итак, интеграл Коши, то есть 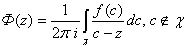
Теорема18: интеграл типа Коши есть функция аналитическая в любой точке своей области определения (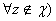 . Более того, эта функция является бесконечно дифференцируемой
. Более того, эта функция является бесконечно дифференцируемой
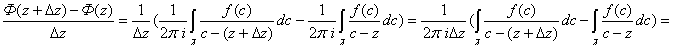
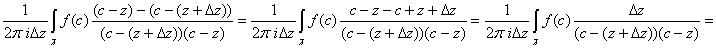
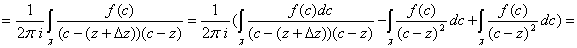
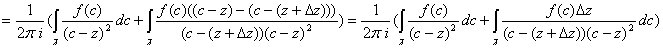
Итак, 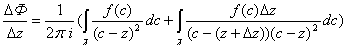
Докажем, что второе слагаемое 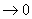 при
при 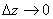 :
:
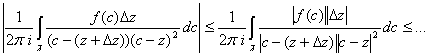
Пусть 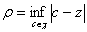 . Тогда
. Тогда 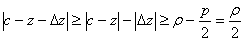
Поскольку 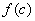 -- непрерывно на
-- непрерывно на 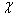 , то оно ограничено на
, то оно ограничено на 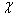 , поэтому
, поэтому 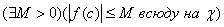
Поэтому 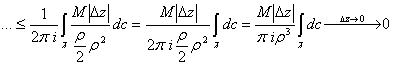
Поэтому 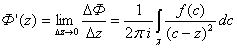
Проведя аналогичные выкладки для 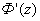 , получаем:
, получаем: 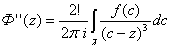
Далее по индукции можно получить: 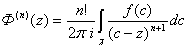
Теорема19: пусть 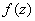 -- аналитична в
-- аналитична в 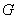 . Тогда она в этой области имеет производные сколь угодно большого порядка
. Тогда она в этой области имеет производные сколь угодно большого порядка
Пусть 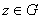 , пусть
, пусть  . Тогда по интегральной формуле Коши,
. Тогда по интегральной формуле Коши, 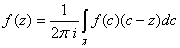
Значит, у нашей функции в точке 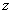 существует производная. По теореме18,
существует производная. По теореме18, 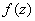 в точке
в точке 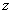 имеет производные сколь угодно большого порядка, причём вычислятся так:
имеет производные сколь угодно большого порядка, причём вычислятся так: 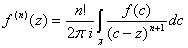
В силу произвольности выбора точки 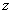 , это верно для любой точки
, это верно для любой точки 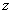 из области
из области 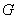
Равномерно сходящиеся ряды аналитических функций
Теорема20: пусть 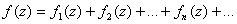 , и члены этого ряда непрерывны на кривой
, и члены этого ряда непрерывны на кривой 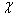 , и ряд равномерно сходится на этой кривой
, и ряд равномерно сходится на этой кривой 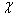 . Тогда данный ряд можно почленно интегрировать вдоль этой кривой, причём справедливо:
. Тогда данный ряд можно почленно интегрировать вдоль этой кривой, причём справедливо: 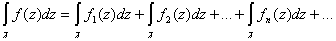
Введём обозначения: 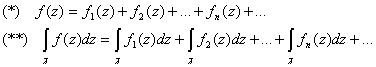
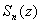 -- частичные суммы ряда (*)
-- частичные суммы ряда (*)
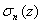 -- частичные суммы ряда (**)
-- частичные суммы ряда (**)
Если (*) -- функциональный ряд, то (**) -- числовой ряд
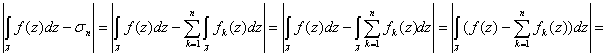
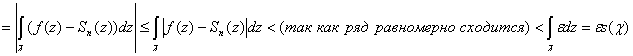
Поэтому 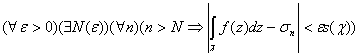
Итак, равномерно сходящиеся ряды мы можем почленно интегрировать
Теорема21: рассмотрим 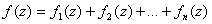
Пусть члены этого ряда есть функции аналитические в области 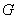 и пусть равномерная сходимость в
и пусть равномерная сходимость в 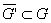 . Тогда
. Тогда 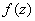 аналитична в
аналитична в 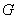 , и данный ряд можно почленно дифференцировать, причём справедливо равенство:
, и данный ряд можно почленно дифференцировать, причём справедливо равенство: 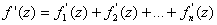
доказательство длинное
Ряд Тейлора
Теорема22: пусть 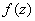 -- аналитична в круге
-- аналитична в круге 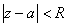
Тогда в этом круге наша функция раскладывается в степенной ряд, причём это разложение единственно
Про границу круга ничего не известно. Поэтому проведём окружность 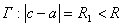 ,
, 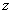 лежит внутри:
лежит внутри:
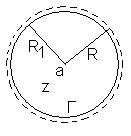
| 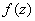 -- аналитична внутри Г и на Г, поэтому по интегральной формуле Коши имеем: -- аналитична внутри Г и на Г, поэтому по интегральной формуле Коши имеем: 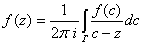
|
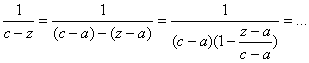
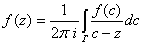 , и пусть
, и пусть 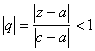 , тогда
, тогда 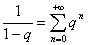
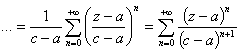
Тогда 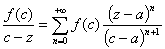
Этот ряд равномерно сходится на 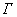 :
: 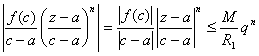 -- этот ряд сходится как геометрическая прогрессия с
-- этот ряд сходится как геометрическая прогрессия с 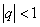 . Тогда по признаку Вейерштрасса, наш ряд
. Тогда по признаку Вейерштрасса, наш ряд 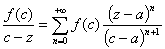 павномерно сходится на
павномерно сходится на 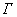
Итак, 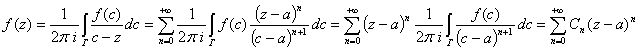
Получим разложение по степеням, при этом 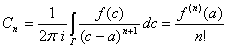
Полученный ряд будет рядом Тейлора, поскольку коэффициенты считаются по такой формуле
Единственность доказывается элементарно.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.