Главная » Общенаучные дисциплины » Математика (3 семестр) » Ряд Лорана.

Ряд Лорана.

Ряд Лорана

Представляет большой практический интерес исследование поведения функции вблизи изолированной особой точки, то есть точки, в окрестности которой функция аналитична, но в самой точке либо не аналитична, либо не определена. Степенной ряд здесь бесполезен, поэтому вводится более общий ряд Лорана:

$\sum_{n=-\infty}^{\infty}c_n(z-z_0)^n$

Если область сходимости ряда Лорана не пуста, она представляет собой круговое кольцо: 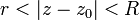$~r<|z-z_0|<R$ .

Основная теорема: если функция $f (z)$ аналитична в круговом кольце, то она может быть представлена в этом кольце сходящимся рядом Лорана, причём однозначно.

Как и для степенного ряда, границы кольца сходимости определяются распределением особых точек функции. По виду ряда Лорана можно сделать некоторые выводы о поведении функции вблизи точки $z 0$ .

Устранимая особая точка: если ряд Лорана не содержит элементов с отрицательными степенями 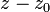$~z-z_0$ . Тогда это просто степенной ряд, определяющий функцию в некотором круге, окружающем 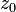$~z_0$ . Сумма ряда в этом круге конечна и может отличаться от $f (z)$ только в точке $z 0$ , так что достаточно переопределить 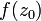$~f(z_0)$ , чтобы функция стала аналитичной во всём круге. Имеет место следующий признак: если функция вблизи $z 0$ аналитична и ограничена, то $z 0$ — устранимая особая точка.
Полюс: если ряд Лорана содержит конечное число элементов с отрицательными степенями 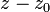$~z-z_0$ . В этом случае функция в точке $z 0$ бесконечна (по модулю).
Существенно особая точка: если ряд Лорана содержит бесконечное число элементов с отрицательными степенями 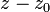$~z-z_0$ . В этом случае функция в точке $z 0$ не может быть корректно определена так, чтобы быть непрерывной.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Дисциплины