Главная » Общенаучные дисциплины » Математика (3 семестр) » Вычет функции.

Вычет функции.

Определение

Вычетом функции $f (z)$ в $a$ называется число

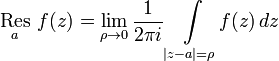$\mathop{\mathrm{Res}}_a\,f(z)=\lim_{\rho\to0}{1\over{2\pi$ .

Вычет в «бесконечности»

Вычетом в бесконечности называется комплексное число, равное

$\mathop{\mathrm{Res}}_\infty\,f(z)=-\lim_{\rho\to\infty}{1\over{2\pi$ .

Вычет дифференциальной формы

Понятие вычета вводится не для функций, а для дифференциальных $(1,\;0)$ -форм на сфере Римана:

$\mathop{\mathrm{Res}}_a\,\omega=\lim_{\rho\to0}{1\over{2\pi$ .

Логарифмические вычеты

Интеграл ${1\over{2\pi$ называется логарифмическим вычетом функции $f (z)$ относительно контура $L$ .

Способы вычисления вычетов

Согласно определению вычет может быть вычислен как контурный интеграл, однако в общем случае это довольно трудоёмко. Поэтому на практике пользуются, в основном, следствиями из определения:

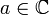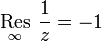В устранимой особой точке $a\in$ , так же как и в точке регулярности, вычет функции $f (z)$ равен нулю. В то же время для бесконечно удалённой точки это утверждение не верно. Например, функция $f(z)=\frac{1}{z}$ имеет в бесконечности нуль первого порядка, однако, $\mathop{\mathrm{Res}}_{\infty}\,\frac1{z}=-1$ . Причина этого в том, что форма $\frac{dz}{z}$ имеет особенность как в нуле, так и в бесконечности.

В полюсе $a$ кратности $n$ вычет может быть вычислен по формуле:

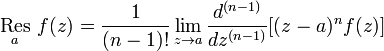$\mathop{\mathrm{Res}}_a\,f(z)={1\over(n-1)!}\lim_{z\to$ ,

частный случай $n = 1$

$\mathop{\mathrm{Res}}_a\,f(z)=\lim_{z\to$ .

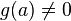Если функция $f(z)=\frac{g(z)}{h(z)}$ имеет простой полюс в точке $a$ , где $g (z)$ и $h (z)$ голоморфные в окрестности $a$ функции, $h (a) = 0$ , $g(a)\neq0$ , то можно использовать более простую формулу:

$\mathop{\mathrm{Res}}_a\,f(z)=\frac{g(a)}{h^\prime(a)}$ .

Очень часто, особенно в случае существенно особых точек, удобно вычислять вычет пользуясь разложением функции в ряд Лорана. Например, $\mathop{\mathrm{Res}}_0\,e^{1/z}=\mathop{\mathrm{Res}}_0\,\left(1+\frac1{z}+\frac1{2!z^2}+\ldots\right)=1$ , так как коэффициент при $z - 1$ равен 1.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Дисциплины