Главная » Общенаучные дисциплины » Математика (3 семестр) » Преобразование Ла-Пласса.

Преобразование Ла-Пласса.

Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию 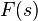$\$ комплексного переменного (изображение) с функцией $\$ вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.

Прямое преобразование Лапласа

Преобразованием Лапласа функции вещественной переменной 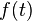$\$ , называется функция 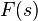$\$ комплексной переменной $s = σ + i ω$ , такая что:

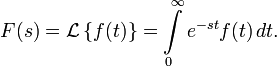
$F(s)=\mathcal{L}\left\{f(t)\right\}=\int\limits_0^\infty$

Правая часть этого выражения называется интегралом Лапласа.

Обратное преобразование Лапласа

Обратным преобразованием Лапласа функции комплексного переменного 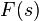$F(s)\$ , называется функция 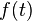$f(t)\$ вещественной переменной, такая что:

$f(t)=\mathcal{L}^{-1}\{F(s)\}=\frac{1}{2\pi$

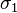где $\sigma_1\$ — некоторое вещественное число (см. условия существования). Правая часть этого выражения называется интегралом Бромвича.

Двустороннее преобразование Лапласа

Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции 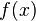$f(x)\$ участвуют значения $x < 0$ .

Двустороннее преобразование Лапласа определяется следующим образом:

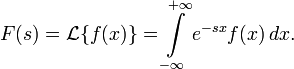
$F(s)=\mathcal{L}\{f(x)\}=\int\limits_{-\infty}^{+\infty}$

Дискретное преобразование Лапласа

Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций.

Различают 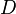$D\$ -преобразование и 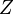$Z\$ -преобразование.

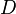$D\$ -преобразование

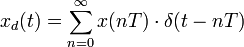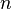Пусть $x_d(t)=\sum\limits_{n=0}^\infty$ — решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени $nT\$ , где $n\$ — целое число, а $T\$ — период дискретизации.

Тогда применяя преобразование Лапласа получим:

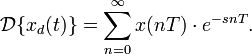
$\mathcal{D}\{x_d(t)\}=\sum\limits_{n=0}^\infty$

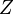$Z\$ -преобразование

Если применить следующую замену переменных:

z = e s T,

получим $Z$ -преобразование:

$\mathcal{Z}\{x_d(t)\}=\sum\limits_{n=0}^\infty$

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Дисциплины