Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция 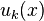 .
.
Равномерная сходимость
Существует функция  такая, что:
такая, что: 
Факт равномерной сходимости последовательности 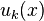 к функции
к функции 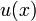 записывается:
записывается: 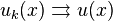
Функциональный ряд

 — n-ная частичная сумма.
— n-ная частичная сумма.
Признак д’Аламбера
Ряд 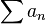
- Сходится абсолютно, если
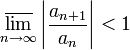
- Расходится, если 1
- Существуют как сходящиеся, так и расходящиеся ряды, для которых

Интегральный признак Коши — Маклорена
Пусть задан ряд  и функция
и функция 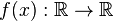 такая, что:
такая, что:
- f(x) нестрого монотонно убывает:
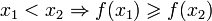
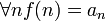
Тогда ряд 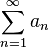 и интеграл
и интеграл 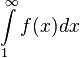 сходятся или расходятся одновременно, причем
сходятся или расходятся одновременно, причем 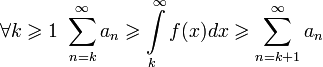
Степенной ряд