Главная » Общенаучные дисциплины » Математика (3 семестр) » Ряды

Ряды

Гармонический ряд

В математике гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда:

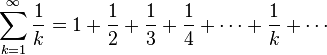$\sum_{k=1}^\mathcal{1}$ .

называется ряд (бесконечная сумма), члены которого образуют геометрическую прогрессию с первым членом а₀ и знаменателем прогрессии, равным q.

Если |q| < 1, то существует предел суммы n первых членов этой прогрессии при неограниченном увеличении количества этих членов n:

В этом случае говорят о бесконечно убывающей геометрической прогрессии.

Ряд назван гармоническим, так как каждый его член, начиная со второго, является гармоническим средним двух соседних.

Обобщенный гармонический ряд

Обобщенным гармоническим рядом (или рядом Дирихле) называют ряд

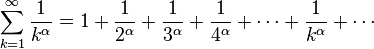$\sum_{k=1}^\infty$ .

Обобщенный гармонический ряд расходится при α≤1 и сходится при α>1.

Сумма обобщённого гармонического ряда порядка α равна значению дзета-функции Римана:

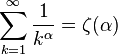
$\sum_{k=1}^\mathcal{1}$

Для чётных это значение явно выражается через число пи, например, 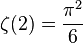$\zeta(2)=\frac{\pi^2}{6}$ , а уже для α=3 его значение аналитически неизвестно.

Сумма ряда

Сумма числового ряда 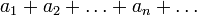$a_1+a_2+\ldots$ определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится. Элементы ряда $a n$ представляют собой либо вещественные, либо комплексные числа.

Сумма (числового) ряда — это предел частичных сумм $S n$ , если он существует и конечен. Таким образом, если существует число 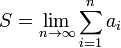$S=\lim_{n\to\infty}\sum_{i=1}^{n}a_i$ , то в этом случае пишут 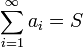$\sum_{i=1}^{\infty}a_i=S$ . Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то говорят, что ряд расходится.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Дисциплины